20080930
オペアンプを使った高次バターワース・フィルタおよび高次チェビシェフ・フィルタの設計方法 - 1 -
ここでは,これらの伝達関数から導き出された数学上のフィルタを,Sallen-Keyおよび多重帰還型フィルタなどを使って,現実の アナログ回路フィルタを構成する方法を解説します.
フィルタの伝達関数と構成回路の伝達関数の関係
一般にカットオフ周波数からバターワース・フィルタやチェビシェフ・フィルタなどを設計する場合,はじめに伝達関数ベースで設計 していきます.各フィルタの伝達関数設計は,上記リンクに詳細を記載していますので参照してみてください. 一般的にバターワース・フィルタやチェビシェフ・フィルタは,フィルタの特性周波数やゲイン・リップル(チェビシェフの場合) から極の位置を算出してフィルタ全体の伝達関数を構成していきます.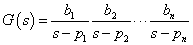
↓
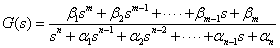
ここでは,Sallen-Keyフィルタや多重帰還型フィルタといった2次フィルタを使用してフィルタを回路として設計していくので, 伝達関数設計時にもともと分解してある1次または2次の伝達関数を,そのまま各1,2次フィルタ回路の設計に利用していきます.
といっても,極の情報だけを渡されてもフィルタ回路の設計はやりにくいので,カットオフ周波数とQ(クオリティー・ファクタ)または 減衰比ζの情報に変換してから設計する方が一般的です.
上記のリンクを辿るとフィルタ全体の特性周波数などのパラメータから,構成される各フィルタ1次または2次のカットオフ周波数と 減衰比ζが算出されるツールを用意していますのでご利用ください.
バターワース・フィルタ
具体的には,バターワース・フィルタのフィルタ次数と減衰比ζの関係は下表の通りです.バターワース・フィルタに構成される, 各フィルタのカットオフ周波数は,フィルタ全体の特性周波数と同値になります.(△20081001下表に追加 奇数フィルタの減衰比を追加と一部訂正)
| 次数 | 減衰比ζ |
| 2 | 0.707 |
| 3 | 0.500 |
| 4 | 0.924 0.383 |
| 5 | 0.809 0.309 |
| 6 | 0.966 0.707 0.259 |
| 7 | 0.901 0.623 0.223 |
| 8 | 0.981 0.831 0.556 0.195 |
| 9 | 0.940 0.766 0.500 0.174 |
| 10 | 0.988 0.891 0.707 0.454 0.156 |
| 11 | 0.959 0.841 0.654 0.415 0.142 |
| 12 | 0.991 0.924 0.793 0.609 0.383 0.131 |
| 13 | 0.971 0.885 0.749 0.568 0.355 0.121 |
| 14 | 0.994 0.944 0.847 0.707 0.532 0.330 0.112 |
もうちょっと有効桁数がほしい場合や,大きな次数の減衰比ζがほしい場合には,バターワース・フィルタを考えるにツールがありますのでご利用ください.
上表に無い奇数のフィルタは,表の2次フィルタ群にさらに1次フィルタを付け加えることになります.伝達関数としては,次の通りです.
[偶数フィルタ]
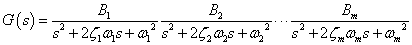
[奇数フィルタ]
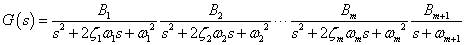
nはフィルタの次数
nが偶数の場合 m=1,2,3・・・n/2
nが奇数の場合 m=1,2,3・・・(n-1)/2
■Sallen-Keyフィルタによってバターワース・フィルタを設計する
Sallen-Keyフィルタによってバターワース・ローパス・フィルタを構成する場合は,下の回路図の通りです.下図の例では,偶数が4次,奇数が5次です.
[偶数]
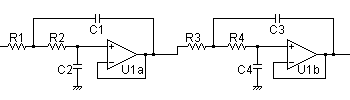
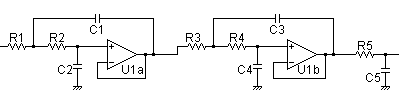
奇数フィルタの場合,1次フィルタは最終段のオペアンプ出力に接続します.もし,Sallen-Keyフィルタの前段に接続すると 1次フィルタのインピーダンスの影響を受けることになりますので,フィルタとしての特性が変化します. ただ,フィルタ出力を低インピーダンスにしたい場合など実践的に,Sallen-Keyなどアクティブ・フィルタの前段にCRフィルタを 配置して,フィルタの特性変化を計算に含めて奇数フィルタを設計することも良くあります.
●カットオフ周波数1kHzの5次バターワース・フィルタ設計例
ここでは,カットオフ周波数1kHzの5次バターワース・フィルタ設計例を示します. 設計条件であるカットオフ周波数fc=1kHzと,減衰比ζは上表のより与えて各フィルタを算出していきます.
最初にU1aの系
(△20081001訂正 :誤ったζの条件を与えていたため下記に誤りがありました.以下のすべての計算結果を書き換えました.)
fc=1kHz ζ=0.809(△20081001誤記訂正)の条件を与えたときのRおよびCの算出
正帰還型ローパス・フィルタ各種計算ツールの結果概要
伝達関数:
R1 = 43kΩ
R2 = 13kΩ
C1 = 0.01uF
C2 = 0.0047uF
遮断周波数(カットオフ周波数)
fc = 981.895565698[Hz]
クオリティ・ファクタ
Q = 0.615841494909
減衰比ζ
ζ = 0.811897223771
極
p = -797.198283823 +573.231016437i[Hz]
|p|= 981.895565698[Hz]
p = -797.198283823-573.231016437i[Hz]
|p|= 981.895565698[Hz]
位相余裕
pm= NAN[deg] (f =0[Hz])
過渡波形に含まれる振動周波数は
f = 573.231016437[Hz]
行き過ぎ量(絶対値で示しています)
第1ピーク gpk = 1.01 (t =0.00088[sec])
第2ピーク gpk = 1 (t =0.0018[sec])
第3ピーク gpk = 1 (t =0.0026[sec])
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = 1
正帰還型ローパス・フィルタ各種計算ツールの結果概要
伝達関数:
| G(s)= |
38061888.6309 s2+10017.8890877s+38061888.6309 |
R1 = 43kΩ
R2 = 13kΩ
C1 = 0.01uF
C2 = 0.0047uF
遮断周波数(カットオフ周波数)
fc = 981.895565698[Hz]
クオリティ・ファクタ
Q = 0.615841494909
減衰比ζ
ζ = 0.811897223771
極
p = -797.198283823 +573.231016437i[Hz]
|p|= 981.895565698[Hz]
p = -797.198283823-573.231016437i[Hz]
|p|= 981.895565698[Hz]
位相余裕
pm= NAN[deg] (f =0[Hz])
過渡波形に含まれる振動周波数は
f = 573.231016437[Hz]
行き過ぎ量(絶対値で示しています)
第1ピーク gpk = 1.01 (t =0.00088[sec])
第2ピーク gpk = 1 (t =0.0018[sec])
第3ピーク gpk = 1 (t =0.0026[sec])
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = 1


つづいて,U1bの系
fc=1kHz ζ=0.309(△20081001誤記訂正)の条件を与えたときのRおよびCの算出
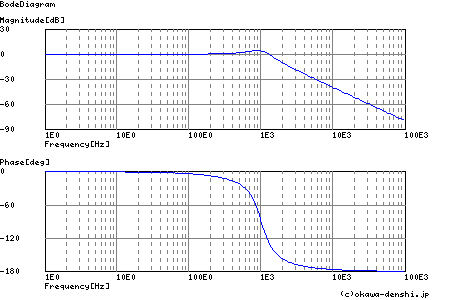
正帰還型ローパス・フィルタ各種計算ツールの結果概要
伝達関数:
R3 = 11kΩ
R4 = 3.3kΩ
C3 = 0.1uF
C4 = 0.0068uF
※パラメータ名をバターワース・フィルタに則して変更しています.
遮断周波数(カットオフ周波数)
fc = 1013.00680494[Hz]
クオリティ・ファクタ
Q = 1.61570778926
減衰比ζ
ζ = 0.30946189857
極
p = -313.48700912 +963.280167948i[Hz]
|p|= 1013.00680494[Hz]
p = -313.48700912-963.280167948i[Hz]
|p|= 1013.00680494[Hz]
位相余裕
pm= 52[deg] (f =1288.1[Hz])
過渡波形に含まれる振動周波数は
f = 963.280167948[Hz]
行き過ぎ量(絶対値で示しています)
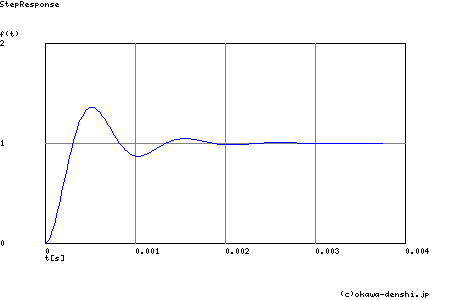
第1ピーク gpk = 1.36 (t =0.00053[sec])
第2ピーク gpk = 0.87 (t =0.001[sec])
第3ピーク gpk = 1.05 (t =0.0016[sec])
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = 1
正帰還型ローパス・フィルタ各種計算ツールの結果概要
伝達関数:
| G(s)= |
40512072.5976 s2+3939.39393939s+40512072.5976 |
R3 = 11kΩ
R4 = 3.3kΩ
C3 = 0.1uF
C4 = 0.0068uF
※パラメータ名をバターワース・フィルタに則して変更しています.
遮断周波数(カットオフ周波数)
fc = 1013.00680494[Hz]
クオリティ・ファクタ
Q = 1.61570778926
減衰比ζ
ζ = 0.30946189857
極
p = -313.48700912 +963.280167948i[Hz]
|p|= 1013.00680494[Hz]
p = -313.48700912-963.280167948i[Hz]
|p|= 1013.00680494[Hz]
位相余裕
pm= 52[deg] (f =1288.1[Hz])
過渡波形に含まれる振動周波数は
f = 963.280167948[Hz]
行き過ぎ量(絶対値で示しています)
第1ピーク gpk = 1.36 (t =0.00053[sec])
第2ピーク gpk = 0.87 (t =0.001[sec])
第3ピーク gpk = 1.05 (t =0.0016[sec])
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = 1


つづいて,CR1次フィルタ
fc=1kHzの条件を与えたときのRおよびCの算出
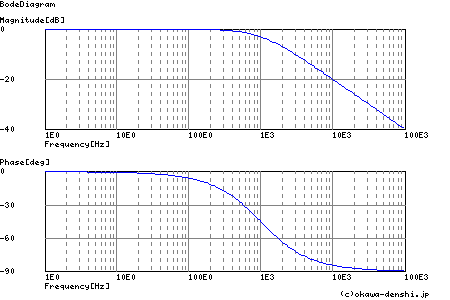
CRローパス・フィルタ計算ツールの結果概要
伝達関数:
R5 = 1.6kΩ
C5 = 0.1uF
※パラメータ名をバターワース・フィルタに則して変更しています.
遮断周波数(カットオフ周波数)
fc = 994.718394324[Hz]
極
p = -994.718394324[Hz]
|p|= 994.718394324[Hz]
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = 1
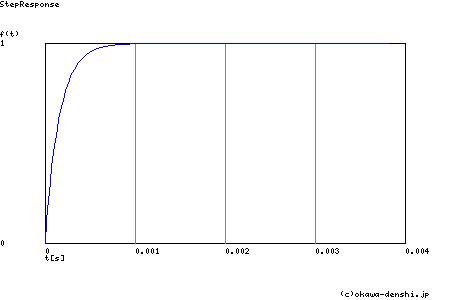
CRローパス・フィルタ計算ツールの結果概要
伝達関数:
| G(s)= |
6250 s+6250 |
R5 = 1.6kΩ
C5 = 0.1uF
※パラメータ名をバターワース・フィルタに則して変更しています.
遮断周波数(カットオフ周波数)
fc = 994.718394324[Hz]
極
p = -994.718394324[Hz]
|p|= 994.718394324[Hz]
Step応答 最終値(t=∞[sec]において収束する場合に有効)
g(∞) = 1


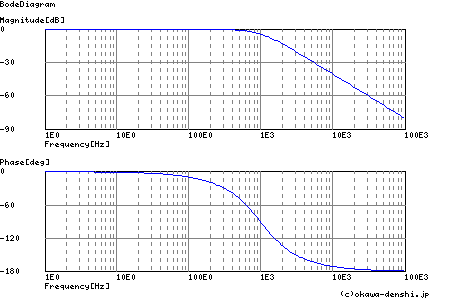
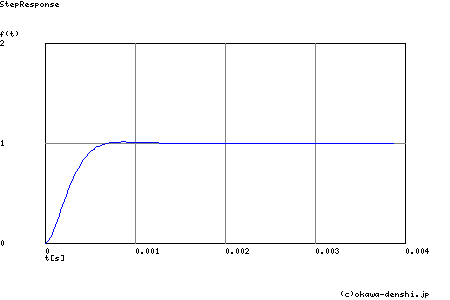
R1〜R5,C1〜C5まで出そろいました.SPICEでシミュレーションすると次のような結果が得られます.オペアンプは理想のオペアンプを 使用しています.
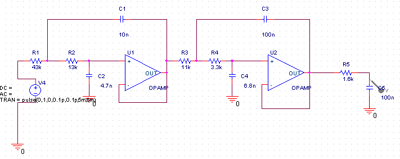
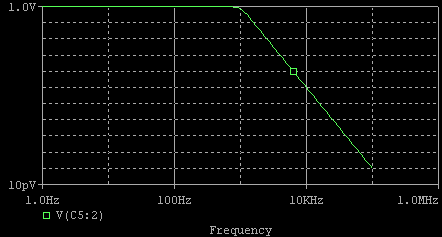
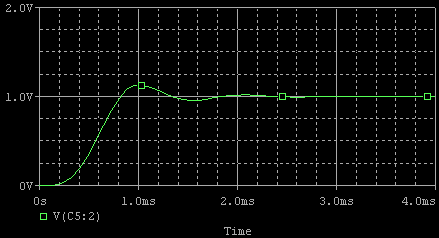
一応5次バターワースについて理論伝達関数から求めた特性(バターワース・フィルタを考えるに掲載のツールによるSim) も掲載しておきます.ほぼ同じ結果を得ています.
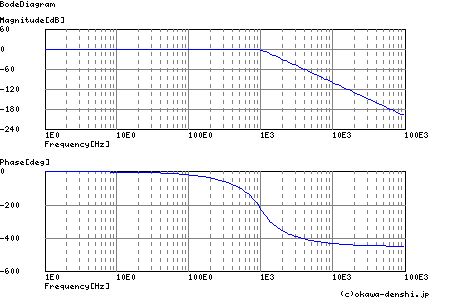
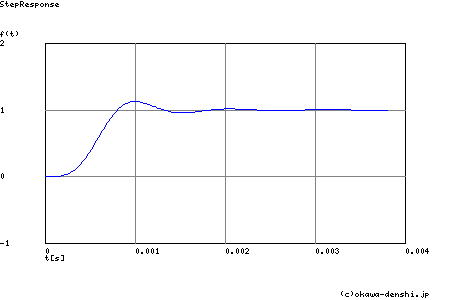
一般的なことですが,市販のオペアンプでフィルタを形成する場合,上記のような理論に則した特性を得られるとは限りません. 現実のオペアンプには,高周波化するほどゲインが小さくなりさらに位相遅れが大きくなりますので,フィルタとしての特性も高周波側の 特性変化が大きくなることはご存知の通りと思います.
あと,高次フィルタ特有の注意点として,構成される2次フィルタに減衰比の小さいものが組み込まれていることに注意をはらう必要 が有ります.上記にもζ=0.309(△20081001誤記訂正)の2次フィルタが組み込まれていますが,このフィルタのSTEP応答をみると激しい振動系であることが わかると思います.このようなオーバーシュートがオペアンプの同相電圧範囲を系の過程で超えない設定にする (充分な電源電圧範囲を確保する)よう気にとめておきましょう.
つづく
[記事URL] http://okawa-denshi.jp/blog/?th=2008093000
カテゴリー:フィルタ(20)
カテゴリー:フィルタ(20)
 前の記事
前の記事