20080708
バターワース・フィルタを考える
前の記事
|
バターワース・フィルタについて バターワース・フィルタというと，ずいぶんと昔には，RF無線回路にバターワース，チェビシェフ，楕円フィルタなどの 高次フィルタをパッシブ(RLC)回路で構成するものがよくあったのですが，十数年くらい前から，セラミック系のフィルタに 置き換わって，最近では一部の無電源系にみられる程度であまり見られなくなっています． しかし，デジタルとのインターフェースで，若干ですが低周波の高次フィルタの用途があるようなので先日公開した伝達関数Widget を使って解説します． たとえばA/Dコンバータの入力にサンプリング周波数の1/2以上の信号が与えられると，エイリアスの問題がありますので 通常ローパス・フィルタを設置しておくことになります．制御（フィードバック）に用いる場合は，１次フィルタ（CRフィルタ）が 限界（２次以上の場合，位相余裕の関係で不安定になりやすい）でしょうが，オープンループの系では，２次以上の高次の ローパス・フィルタが用いられることもあるようなのでそのような際によく用いられるバターワース・フィルタについて解説します．
■バターワース・フィルタと伝達関数解析
|
伝達関数Widgetです ↓ |
・伝達関数Widgetの基本的な使い方／解説はこちらを参照してください．
・伝達関数WidgetのAPIなどの仕様および遠隔操作の方法はこちらを参照してください．
・伝達関数WidgetのAPIを使った簡単なサンプルはこちらを参照してください．
・伝達関数Widgetのコードの取得はこちらを参照してください．
バターワース・フィルタは，CRフィルタのようななだらかな周波数特性を描き，透過域では周波数によるゲインの変化が小さく 周波数変化に対するゲインの増減の方向が一定（ローパス・フィルタであれば周波数が大きく変化すればゲインは小さくなり， ハイパス・フィルタであれば周波数が大きく変化すれば，ゲインは大きくなります．） 遮断域ではフィルタの次数に応じた減衰特性が得られるフィルタです．発想がCRフィルタの延長上で高次に対応させたようなフィルタで， 考え方がシンプルです．
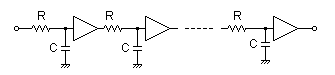
仮に上図のように一次フィルタ（CRフィルタなど）だけで多段に接続して高次フィルタを構成した場合，下図の周波数特性のように 肩の丸いフィルタになります．（必ずしも肩の丸いフィルタが悪いことはありません）
−Butterworth 4次 −一次フィルタ多段 4次
バターワースの肩は，どのようにつくるのか？ といいますと二次フィルタの多段によって構成して，減衰比ζの設定によって カットオフ周波数のゲインを適度に調整する訳です．このとき，バターワース・フィルタを構成するすべてのフィルタは， カットオフ周波数をωcに一致させて設定します．
| → |
|
→ |
|
→・・・→ |
|
→ |
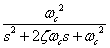
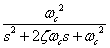
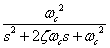
上図はフィルタの次数が偶数の場合で，奇数の場合には，上系にさらに一次フィルタが直列に追加されます．
上図のような二次フィルタ多段の系において，フィルタ全体の伝達関数は次式のようになります．
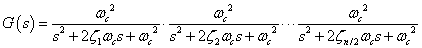
nはフィルタの次数
これをフーリエ変換して
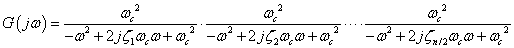
カットオフ周波数ωcにおけるゲインを求めると
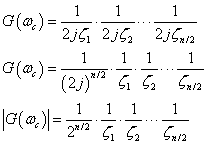
ということで上の式が二次フィルタ多段の系における，カットオフ周波数のゲインということです．よってあとは適当に ζ1からζn/2まで決めてやれば良いのです．しかし，構成されているうちのある二次系フィルタの減衰比がζ > 1ですと その二次系フィルタは２つの実数極をもってしまい，カットオフ周波数の異なる２つの一次フィルタの接続と同じになってしまいます ので，ζ < 1とします．
ζ < 1であってもζの偏りによってBode線図やStep応答が不自然になる場合があります．そこでバターワース・フィルタでは， ζの値を適度に分散させるべく，極の配置を次のように設定されます．
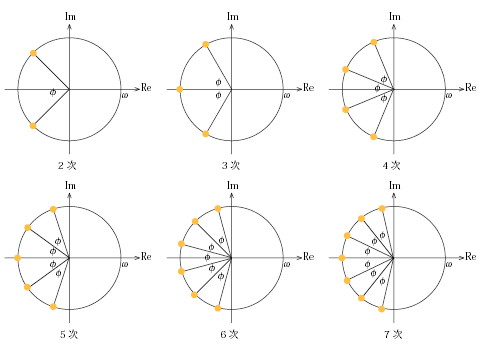
バターワース・フィルタの極配置 (●が極)
φ=π／n nはフィルタの次数
ここでバターワース・フィルタの極は，
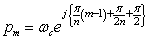m=1,2,3・・・n
■減衰比ζと極位置の関係
極の位置と減衰比ζとは密接な関係があります．ある二次フィルタの極をp1，p2とすると
p1=ωce jθ=ωc(cos θ+ j sin θ)
p2=ωce -jθ=ωc(cos θ- j sin θ)
p1，p2を使って二次フィルタの伝達関数の分母を示すと
[分母]=(s-p1)(s-p2)
= s2 -(p1+p2)s + p1p2
= s2 -{ωc(cos θ+ j sin θ) + ωc(cos θ- j sin θ)} s + ωc2(cos θ+ j sin θ)(cos θ- j sin θ)
= s2 - 2cos θωc s + ωc2
二次フィルタの伝達関数の分母の一般式は s2 + 2ζ ωc s + ωc2ですので
ζ = -cos θ
ということです．
よって上図バターワース・フィルタの極配置から，ζ は極の実数成分／ωcと等しいのです．
極の位置と減衰比ζとは密接な関係があります．ある二次フィルタの極をp1，p2とすると
p1=ωce jθ=ωc(cos θ+ j sin θ)
p2=ωce -jθ=ωc(cos θ- j sin θ)
p1，p2を使って二次フィルタの伝達関数の分母を示すと
[分母]=(s-p1)(s-p2)
= s2 -(p1+p2)s + p1p2
= s2 -{ωc(cos θ+ j sin θ) + ωc(cos θ- j sin θ)} s + ωc2(cos θ+ j sin θ)(cos θ- j sin θ)
= s2 - 2cos θωc s + ωc2
二次フィルタの伝達関数の分母の一般式は s2 + 2ζ ωc s + ωc2ですので
ζ = -cos θ
ということです．
よって上図バターワース・フィルタの極配置から，ζ は極の実数成分／ωcと等しいのです．
上の解説を踏まえ，バターワースの極の式から減衰比を求めると，
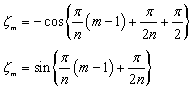
nはフィルタの次数
nが偶数の場合 m=1,2,3・・・n/2
nが奇数の場合 m=1,2,3・・・(n-1)/2
ということで，バターワースの減衰比ζの数値列を計算させる，ツールを置きました．ご活用ください．
↓
■n次バターワース・フィルタを構成する二次フィルタの減衰比
※これはWidgetとは無関係，次数を与えて[計算]ボタンをクリックすると，次数に応じてζ が計算され列挙されます．
計算式は上のζ mの代数式に従っています．
■バターワース・フィルタの使用上の注意点
バターワースの肩は，どのようにつくるのか？というところで触れていますが，二次フィルタの減衰比ζの設定によって カットオフ周波数のゲインを調整しています．さらにバターワースを構成している二次フィルタの減衰比ζは， ζ < 1ですべて振動系なのです．
とくに次数が偶数のバターワース・フィルタは，完全な振動系になります．下図がCR多段とバターワースのSTEP応答を比較したものです．
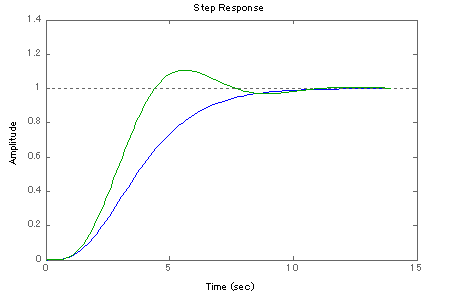
−Butterworth 4次 −一次フィルタ多段 4次
バターワースの肩は，あのオーバーシュートのために設定されているようなもの？なのですが，そもそもフィルタって振動の除去を目的としている のですから，フィルタを設計する以上，このフィルタ自身がωc振動の増幅（発信源）として働く側面も知っておくことは必要です．
さらに，このフィルタに求められる立ち上がり時間（Rise time）仕様が，80%位に敷居値を設けていたならバターワースの方がはるかに 優れていますが，98%位に敷居値を設けていたなら上図8〜10[sec]のあたりになるのですがバターワースの方が劣る部分もある のです．
言いたいことは，要するにどんなフィルタも一長一短があります．よく特徴を知って設計に生かし組み込むことが大切です． とくに仕様がバターワースとして限定されないのであれば，ζの値をちょっとずつ変えてオーバーシュートを制限することも可能です． 大切なことは，ちょっと知っていればバターワースの亜種（工夫）も容易にできると言うことです．さらに回路も工夫して， 二次フィルタにTwin-Tノッチフィルタを組み合わせて遮断特性を改善するということも可能ですので そちらも参考にしてみてください．
※伝達関数Widgetは技術解説にも使えます．ので，ぜひ利用してみてください．