1.  前の記事
2. 次の記事 

■伝達関数の周波数軸方向への移動（特性そのままfc変換）

アナログフィルタ回路の設計は，伝達関数の設計から行うことが多いと思います．基本的なフィルタ回路を使用する場合，その伝達関数は 良く知られていますが，正規化されている式も多くあります．正規化とは，例えば次のような伝達関数です．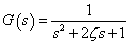
            −−(1)
上の(1)式を一般化して特性周波数を与えられる代数式にすると次式のようになります．
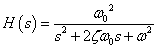            −−(2)
正規化された伝達関数はω₀=1[rad/s]の場合を言います． ここでは，正規化式(1)から(2)式への変換について，フィルタの特徴を変えずに（例えばバターワースであればバターワースのまま） 周波数のみを変更する算術的方法を解説します．

---

まず，(1)式の引数 s に操作を加えます．
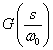            −−(3)
この操作によってGは，周波数方向に1/ω₀に圧縮されます． (3)式に|s|=ω₀を代入した場合，(1)式において|s|=1を代入した場合と 全く同等になることがわかると思います．つまり周波数軸方向に特性をω₀分 平行移動することになります．

(3)を計算すると次式の通りです．
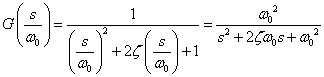            −−(4)
(4)式は(2)一般式と同じになります．

ここでは２次伝達関数について解説しましたが，１次であっても３次以上であっても，(3)式の変換によって周波数軸方向へのスライドが 可能です．



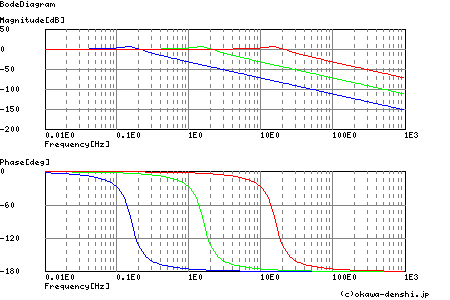
上図は，２次伝達関数の例です．青，緑，赤はそれぞれω₀＝1，10，100[rad/s]に対応しています．青は正規化されて いる伝達関数で，それ以外は(3)式によって周波数軸方向へスライドさせている例です．

ここで紹介した周波数変換はこちらの伝達関数ツールにて自動計算ツールを公開しています．そちらもご利用下さい．