伝達関数の算術的 周波数変換について2
前の記事
伝達関数の算術的 周波数変換について，前回は，周波数特性などの特性を変えず，そのまま周波数軸方向（logスケールで）に平行移動するための算術的な方法を 紹介しました．前回の記事はこちらです．→伝達関数の周波数軸方向への移動（特性そのままfc変換）
今回の記事は，伝達関数の算術的 周波数変換の続編で，ある周波数を対称軸として線対称となる伝達関数に変換する方法を解説します．
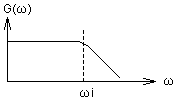 LPF |
→ ← |
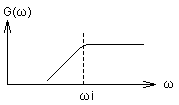 HPF |
| 図 伝達関数の周波数特性例 | ||
上図左のような周波数特性をもつ伝達関数があった場合，算術的に 上図右のような伝達関数に変換する方法です．一般的に， もともとＬＰＦ（ローパス・フィルタ）の特性を持っている伝達関数の場合は，ＨＰＦ（ハイパス・フィルタ）に変換され， ＨＰＦの特性を持っている伝達関数の場合は，ＬＰＦ（ハイパス・フィルタ）に変換されます．
具体的な算術方法は，G(s) という正規化された伝達関数があった場合，G(s)の引数に次のような操作をします．
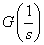−−(1)(1)式に|s|=ωを代入（簡易的なフーリエ変換）した場合に，
周波数特性においては，ω＝1[rad/s]を対称軸として，線対称（鏡映しのよう）に特性が
反転します．理由は，周波数軸をlogスケールとした場合のωは，
log(1/ω)＝-log(ω)
なので，周波数軸がω＝1[rad/s]を挟んで正負が反転するためです．
■一次伝達関数の変換例
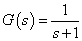−−(2)たとえば，上式(2)で与えられる正規化一次ローパス・フィルタは，(1)式のような操作をすると次式(3)のように変換されます．
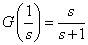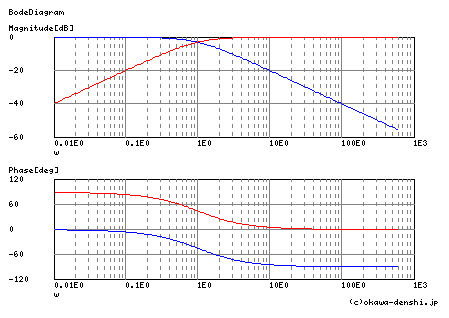
−−(3)式(2)，式(3)伝達関数をBode線図によって示すと次の通りです．
− (2)式 LPF
− (3)式 HPF
青が(2)LPF，赤が変換後 (3)HPFです．ω=1[rad/s]を対称軸として線対称に 変換されている様子がわかると思います．（LPFがHPFに変換されます．）
■二次伝達関数の変換例
つづいて，二次伝達関数についても同様に検証します．
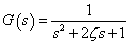−−(4)上式(4)は正規化された二次LPFの伝達関数です．式(4)に，(1)の算術的操作を与えると次式(5)のように変換されます．
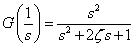−−(5)式(5)は，正規化された二次HPFの伝達関数になります．式(4)，式(5)伝達関数をBode線図によって示すと次の通りです．
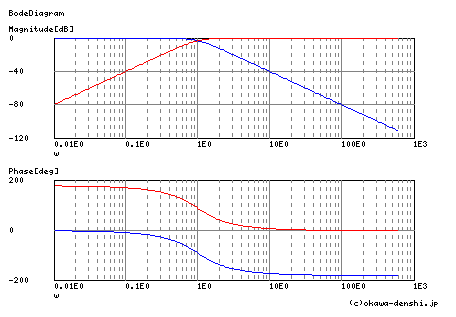
− (4)式 LPF
− (5)式 HPF
青が(4)LPF，赤が変換後 (5)HPFです．ω=1[rad/s]を対称軸として線対称に 変換されている様子がわかると思います．変換前後でLPFからHPFに変換されますが，ζ の値が 保たれる特徴があります．このため，この変換による伝達関数の振動特性は変化しません．
この記事では，一次，および，二次伝達関数のみ例として扱いましたが，三次以上の伝達関数についても，同様に(1)式の周波数操作を利用できます． 三次以上のすべての遅延系伝達関数は，一次伝達関数と二次伝達関数の和によって表すことができます ので，一次伝達関数と二次伝達関数の和に表せば，三次以上についても，(1)式の算術的周波数操作を利用できることがわかると思います．
さらに，この記事では，対称軸ω=1 の場合のみを扱いましたが，任意の周波数でも
正規化の手順を踏めば利用できます．手順は次の通りです．
- 正規化する：特性周波数をω=1 に変換（具体的方法はこちら→周波数軸方向への平行移動）
- 上記式(1)の変換
- 1の手順で正規化された伝達関数を，元の特性周波数に戻す
このような手順を自動化して伝達関数の周波数変換を実行できるツールを，こちらに（伝達関数ツール）公開していますのでご利用ください．