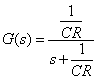2次系伝達関数の特徴
2次系(1)伝達関数について振動に関する特徴を考えます.ここであつかう伝達関数は数学的な一般式として,伝達関数式を構成するパラメータと物理的な特徴との関係を導きます.
ここでは,式2-3-30が2次系伝達関数の一般式として話を進めます.
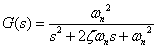 |
式2-3-30 |
まず,伝達関数パラメータと極の関係を確認しましょう.式2-3-30をフーリエ変換すると(ラプラス関数のフーリエ変換はこちら参照)
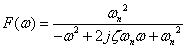 |
式2-3-31 |
極は伝達関数の利得が∞倍の点なので,[分母]=0より極の周波数ωkは
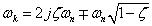 |
式2-3-32 |
式2-3-32の極の一般解には,虚数が含まれています.物理現象における周波数は虚数を含みませんので,物理解としては虚数を含まない条件を解とする必要があります.よって式2-3-30の極周波数ωkは,ζ=0の条件におけるωk=ωnのみとなります(ちなみにこの条件をRLC直列回路に見立てるとR=0の条件に相当).
つづいてζ=0以外の条件での振動条件を考えます.まず,式2-3-30から単位インパルスの過渡応答を導きましょう.
インパルス応答を考える理由は,単位インパルス関数は,-∞〜+∞[rad/s]の範囲の余弦波(振幅1)を均一に合成した関数であるため,インパルスの過渡応答関数が得られれば,-∞〜+∞[rad/s]の範囲の余弦波のそれぞれの過渡応答の合成波形が得られることになり,伝達関数の物理的な特徴をとらえることができます.
たとえば,インパルス過渡応答関数に,sinまたはcosが含まれるか否かによって振動の有無,あるいは特定の振動周波数を数学的に抽出することができます.
この方法は,以前2次系システム(RLC回路の過渡)のSTEP応答に関する記事で,過渡電流が振動する条件と振動しない条件があることを解説しました.(詳細はこちら)
ここでも同様の方法で,振動条件を抽出していきます.まず,式2-3-30から単位インパルス応答関数を求めます.
| C(s)=G(s)R(s) | 式2-3-33 |
R(s)は伝達システムへの入力関数で単位インパルス関数です.
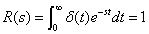 |
式2-3-34 |
より
| C(s)=G(s) | 式2-3-35 |
単位インパルス応答関数は伝達関数そのものとなります(伝達関数の定義の通りですが).
そこで,式2-3-30を逆ラプラス変換して,時間領域の過渡関数に変換すると(計算過程はこちら)
| 条件 | 単位インパルスの過渡応答関数 | |
| |ζ|<1 ただし ζ≠0 |
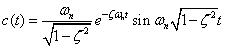 |
式2-3-36 |
| |ζ|>1 | 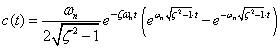 |
式2-3-37 |
| ζ=1 | 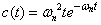 |
式2-3-38 |
表2-3-1 2次伝達関数のインパルス応答と振動条件
|ζ|<1で振動となりζが振動に関与していることが分かると思います.さらに式2-3-36および式2-3-37より,ζが負になる条件(ζ<0)で,eの指数が正となることから t→∞ で発散することが分かります.
ちなみにωnを固定角周波数,ζを減衰比(damping ratio)といいます.