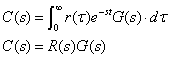伝達関数
ある伝達システム(回路)の信号伝達に関して,入力信号と出力信号の関係を数学的に求めてみました.(→詳細こちら)ここでは入出力の関係をもうちょっと便利な形で示してみようと思います.

図2-3-7 伝達回路と入出力信号
図2-3-7の入力信号 r(t) と出力信号 c(t)と伝達回路のインパルス応答関数 g(t) の関係を数式でしめすと次の関係がありました.
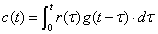 |
式2-3-5 |
式2-3-5の関係(たたみ込み積分)をラプラス変換すると,ラプラス変換表(表2-1-4)のNo.12項より次の関係が得られます.
| C(s)=G(s)R(s) | 式2-3-7 |
式2-3-7は,入力関数と出力関数をそれぞれのラプラス関数R(s),C(s)が,インパルス応答関数のラプラス関数 G(s)との積によって完結に示すことができます.

図2-3-8 伝達回路と入出力信号
ここで,インパルス応答関数のラプラス関数 G(s)を伝達関数といいます.
(1)たたみ込み積分のラプラス変換
式2-3-5(下式)たたみ込み積分のラプラス変換について説明します.
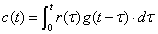 |
式2-3-5 |
ラプラス変換表を使えば式2-3-7のように簡単にラプラス変換できますが,ここではラプラス積分から式2-3-7を導いてみたいと思います.式2-3-5のラプラス変換をラプラス積分によって示すと
| |
式2-3-6 |
この式はこのままでは解きにくいので積分順位を変更して解きやすくします.
内側の積分に着目すると τ は,0〜t の積分範囲なので
0 ≦ τ ≦ t
この関係をグラフに示すと,下図のように積分範囲はグレーの塗りつぶしたエリアが相当します.
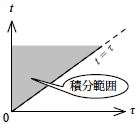
図2-3-9 たたみ込み積分の積分範囲
式2-3-6の積分では,内側の積分(τの積分)を最初に行い,次に外側の積分(t の積分)をしています.
図2-3-9の積分範囲を網羅すれば積分方法(経路)は一般に問わないので次のように積分経路を変更したいと思います.
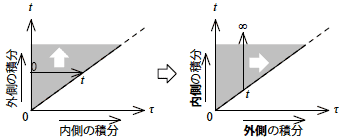
図2-3-10 積分範囲の変更
式2-3-6内側の積分では,図2-3-10(左)に示すようにτについて 0〜 t を積分して,続いてその積分値を t について0〜∞ にて積分していました.
この積分経路を図2-3-10(右)のように,最初に t について t〜∞ を積分して,続いて τについて 0〜∞ の範囲を積分する経路に変更しましょう.すると式2-3-6は次のように積分の順序を変更することが出来ます.
| |
式2-3-7 |
式2-3-7の形になればラプラス変換しやすくなります.ここで内側 t の積分について,ラプラス変換表(表2-1-4の4項)に適合させるよう変形していきます.
| No | 時間関数 | ラプラス関数 |
| 4 | e-saF(s) |
式2-3-7の内側の積分(tの積分)の積分範囲が通常のラプラス積分範囲(0〜∞)と異なりますので次のように展開します.
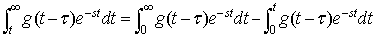
ここでg(t - τ)を下記のように定義すると
|
![]()
すると式2-3-7は