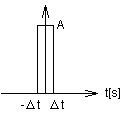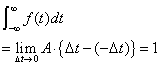たたみ込み積分
入力信号に応じて出力信号が得られる伝達回路を想定します.この伝達回路は電子回路を想定していますが,機械系や化学系など物理系の伝達モデルであれば,いずれの場合も同様に考えることができます.
この伝達回路に入力信号(関数)r(t) を与えたときに得られる出力信号(関数)を c(t)としたとき,r(t) とc(t) の関係を数学的に考えましょう.
一般に入力信号が異なれば出力信号も異なる場合が普通で,任意の入力信号に対応したシステム(伝達回路)の伝達特性を数学的に知るためには,一義的な入出力の関係に置き換えることが必要です.
その方法は
1.入力信号をインパルス関数(1)に複数分割(右記参照)
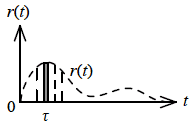
図2-3-4 信号をインパルス関数に分解
図2-3-4のように信号を矩形形状に分割することで,入力信号 r(t)がどのような入力信号(関数)であっても,複数の分割されたインパルス関数として考えることができます.
分割されたインパルス関数を f(τ) とすると,t = τ において,
f(τ)=r(τ)·∆τ·δ(t-τ) 式2-3-1
ここで ∆τはインパルスの幅です.右記の図2-3-3でいうと{∆t-(-∆t)}です.
2.インパルス入力に対する応答関数を定義する
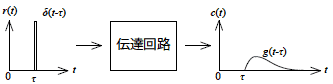
図2-3-5 インパルス応答
その入力関数から得られる出力関数も同一の関数 g(t)が出力されるものとして考えます.このインパルス応答関数が伝達回路の特性に重要な意味をもちます.
3.分割された複数のインパルス応答関数から出力信号を復元
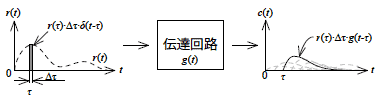
図2-3-6 複数のインパルス応答と出力信号の合成
それぞれの分割されたインパルスがつくる応答が出力で重なり合って(足し合わされて),出力信号 c(t) がつくられます.以上を数式によって示すと
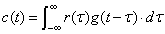 |
式2-3-2 |
r(t) は t≧0の関数であるので
| r(t)=0 (t<0) | 式2-3-3 |
式2-3-3より,積分範囲を [0:∞]とします.
さらに,物理系の応答で,伝達回路の出力が入力信号を与えられる時点より以前に影響をうけることはないので,g(t) は時間 τ以前 (t<τ) で
| g(t-τ)=0 (t<τ) | 式2-3-4 |
よって,式2-3-2の c(t) は,τが tより大きい範囲(t<τ)において0となるので,積分範囲は[0:t]とすることができます.
この積分範囲を反映すると式2-3-2は
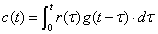 |
式2-3-5 |
1〜3の考え方を経て伝達回路の信号伝達に関する関係を,インパルス関数g(t)の介在をすることによって数学的に求めることができました.ここで式2-3-5の関係を
| c(t)=g(t) * r(t) | 式2-3-6 |
と略して書くこともできます.ちなみに * はアスタリスクで乗算の意味とは異なります.式2-3-5,式2-3-6の積分をたたみ込み積分といいます.