ラプラス変換表
ラプラス変換の対応表を次に示します．この対応表に従って変換する場合は，積分計算が不要です．ラプラス変換をする場合，このような表に対応させて変換するのが一般的です．
(1) 具体的な時間関数とラプラス変換の対応
| No | f(t) | F(s) |
| 1 | 1 |  |
| 2 | t |  |
| 3 | tn |  |
| 4 | eat |  |
| 5 | sin at |  |
| 6 | cos at |  |
| 7 | ebt sin at |  |
| 8 | ebt cos at |  |
| 9 | sinh at |  |
| 10 | cosh at |  |
| 11 | t eat |  |
| 12 | t sin at |  |
| 13 | t cos at |  |
| 14 |  |
 |
| 15 |  |
1 |
| 16 | tx |  |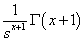
表2-1-3 ラプラス変換表
(2) 一般時間関数とラプラス変換の対応
| No | 時間関数 | F(s) |
| 1 | a f(t) + b g(t) | a F(s) + b G(s) |
| 2 | f(at) |  |
| 3 | eat f(t) | F(s-a) |
| 4 |  |
e-saF(s) |
| 5 | f'(t) | sF(s)-f(0) |
| 6 | f''(t) | s2F(s)-sf(0)-f'(0) |
| 7 | f(n)(t) | snF(s) - sn-1f(0) - sn-2f'(0) - ・・・sf(n-2)(0) - f(n-1)(0) |
| 8 |  |
 |
| 9 |  |
 |
| 10 |  |
 |
| 11 |  |
 |
| 12 |  |
F(s)G(s) |
| 13 | -tf(t) | F'(s) |
| 14 | (-t)nf(t) | F(n)(s) |
| 15 |  |
 |
△2008/11/11 読者からのご指摘で(2)-1を誤記訂正しました.ご指摘ありがとうございます
表2-1-4 一般関数のラプラス変換表
【質問】2008/02/04
(1)（表2-1-3）の７の符号が＋、−入れ替わった場合どのようになるのですか？
【回答】2008/02/04
表中の７項に限りませんが，a および bは実数（複素数でない連続した数）です．実数は，正も負もとり得るので，それぞれ負の値（変数）を代入（例：a= -α，b= -β）してみてください．
【追加】2008/02/08
ご質問に関して，たとえば
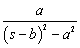のラプラス逆変換といった意味合いと推測すると．．．一般的な２次系以上のラプラス逆変換は，s の関数を部分分数分解して，表2-1-3の４項に該当させる形にして逆変換します．具体例としては２次系であればこちらを参照してください．また，高次であればこちらを参照してください．
【質問】2009/05/30
√t のラプラス変換はどうなるのでしょう？
【回答】2008/06/08
回答はこちらに掲載しました．これに関連してラプラス変換表(1)の16を追加しました．