RLC回路の過渡

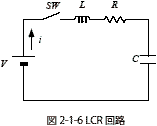
図2-1-6のＲＬＣ回路についてSWを通電させた際の過渡電流 i をラプラス変換を使って求めてみましょう．コイルL，抵抗R，コンデンサCそれぞれにかかる電圧をv_L，v_R，v_Cとすると式2-1-23の関係があります．

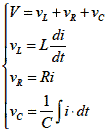式2-1-23

上式からv_L，v_C，v_R を消すと

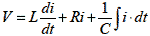式2-1-24

ラプラス変換すると

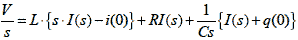式2-1-25

q(0) はt=0 におけるコンデンサC の充電電荷でq(0)=0 ，またi(0) はt=0 におけるコイルL の電流でi(0)=0 とすると，I(s)は式2-1-26のようになります．

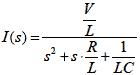式2-1-26

ここからラプラス逆変換をして時間領域の関数に戻します．

この式のままではラプラス変換表（表2-1-3，表2-1-4） にぴったり適合するものはありません．この式に変更を加えて表に適合する形をつくる必要があります．そこで，I(s) の分母を因数分解し，部分分数をつくることによって表2-1-3 の4（下表参照）に適合する形をつくっていきます．

No	f(t)	F(s)
4	eat

表2-1-3抜粋

まず式2-1-26 の分母を因数分解して(s-α)(s-β)の形をつくり，部分分数に分解していきます．

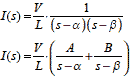式2-1-27

ここで，各パラメータ（Ａ，Ｂ，α，β）を計算していきます．

この式中のα，β は2 次方程式の解として与えられるので，仮にs に関する２次方程式をs²+bs+c=0 としたとき，α およびβ は式2-1-28の関係があります．

α，β＝

式2-1-28

つづいて式2-1-27 のA，B について求めます．A，B は式2-1-27を分母を共有化して式2-1-26のもとの形に戻したとき，それぞれの項（s²+bs+cのb，c）に対応して等式をつくることによって求めることができます．

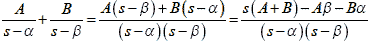
式2-1-29の分子と式2-1-26の分子を対応させて，s(A+B)＋(-Aβ-Bα)＝0s＋1とすると

式2-1-30

これを解くとA，Bは

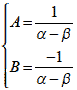式2-1-31

となります．ちなみに部分分数におけるA，B を留数⁽¹⁾ といいます．

つづいてαおよびβは，式2-1-28より

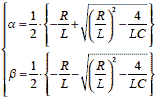式2-1-32

つづいて式2-1-27にA，B（式2-1-31）を代入するとI(s)は，

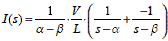式2-1-33

この形になれば，表2-1-3 の4に適合するのでラプラス逆変換ができます．ラプラス逆変換すると

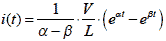式2-1-34

α，βを代入すると

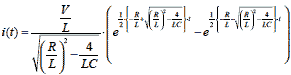
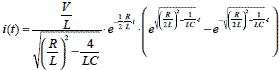式2-1-35

過渡電流 i を求めることができました．

← 戻る  1  2  次へ →