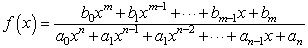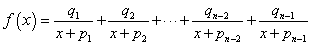留数定理
(1)留数定理についての解説
次式についての部分分数分解を考えます.
![]()
この式の分母を因数分解していきます.
![]()
(1)式が次式のような部分分数に変換が可能であるとき
![]()
b1,b2,・・・,bnを留数といいます.一般に留数bxは(3)式の関係があります.
![]()
(3)の関係を留数定理と言います.
ここではY(s)について,分子を1としていますが,分子はsの関数としても部分分数分解が可能です.その場合,分子の関数の次数が,分母の次数よりも小さい条件となります.
留数定理について
(2)式について両辺に(s+a1)をかけると
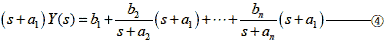
ここで,式(4)のs に-a1を代入すると(s+a1) が0 になるので式(4)の右辺はb1 のみが残ります.
左式は,Y(s)のsに-a1 を代入すると分母が0になるので直接代入できませんので極限値をとります.その結果が(3)式(留数定理)です.sの次数が高くなると方程式では解きにくいのでこの定理が有効です.