極位置と伝達関数の特徴2
n次系伝達関数の一般式を次の式2-3-40としたとき,この伝達関数の発散・収束,振動について考えます.
| |
式2-3-40 |
式2-3-40を部分分数に分解します.(部分分数についてはこちらを参照)
| |
式2-3-41 |
式2-3-41のpxは伝達関数G(s)の極になります.この伝達関数G(s)の単位インパルス応答から特徴を考えます.式2-3-41からインパルス過渡応答を導くと,ラプラス変換表(表2-1-3のNo.4)より
| |
式2-3-42 |
式2-3-42のように eの指数関数になります.ここで,pxは一般に複素数です.pxを次のように置くと
px=σx+jωx
式2-3-42は
| |
式2-3-43 |
ここで極 pの実数部σに着目すると,t → ∞で
σx > 0 で発散
σx < 0 で収束
σx = 0 で無減衰
の特徴が分かると思います.
続いて,振動について考えます.振動はインパルス応答過渡関数にsinなど振動要素が含まれます.
そこで,先に説明した2次系伝達関数と振動の関係を応用していきます.式2-3-41について,ある2点の極 pk,pl(の項)を使って2次系伝達関数の要素を次のように抽出していきます.
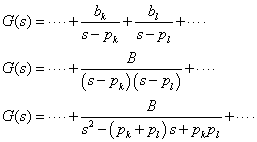
この式を次のように置くと.
| |
式2-3-44 |
このように2次系伝達関数を伝達関数G(s)に含めて重ね合わせとして考えることができ,2次系伝達関数の特徴(極位置またはζと振動との関係)を踏まえて考えることができます.詳細はすでに説明していますのでこちらを参照.