極位置と伝達関数の特徴

２次系伝達関数について下の式2-3-30を一般式としたとき，ζと振動の関係を示しました（詳細こちら）．

式2-3-30

ここでは先の２次系伝達関数の特徴と減衰比ζの関係を踏まえて，伝達関数の極の位置とζとの関係を示し，その上で極位置と伝達関数の特徴を考えていきます．

まず，式2-3-30の伝達関数についてs 領域における極を求めていきます．極をp とすると

式2-3-39

この関係（式2-3-39）に，先に求めたζと伝達関数の物理的特徴をあてはめると，極の複素平面上の位置と伝達関数の物理的特徴に相関性が伺えます．ω_n＞0とすると

減衰比の範囲	極の位置	特徴
ζ < 0	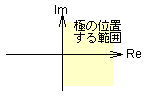図2-3-22	［発散］ ζ < 0では，式2-3-36〜38より e の指数がプラスになるため t → ∞で発散
ζ = 0	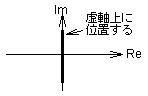図2-3-23	［無減衰］ ζ =0では，式2-3-36より時間変化による振幅の変動（減衰）がない．
ζ > 0	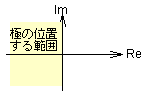図2-3-24	［収束］ ζ >0では，式2-3-36〜38より e の指数がマイナスになるため t →∞で収束

表2-3-3 極の位置と伝達関数の特徴１

つづいて振動に関して，極位置との関係は

減衰比の範囲	極の位置	特徴
\|ζ\| <1	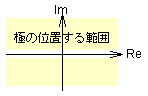図2-3-25	［振動］式2-3-36より，極は実数軸をはさみ線対称に位置
ζ =1	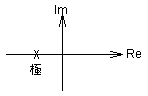図2-3-26	［臨界減衰］極は実数軸上に一点のみ位置する．ζ=1の場合，極は虚軸より左（σ<0）．ζ=-1の場合，極は虚軸より右（σ>0）
\|ζ\| >1	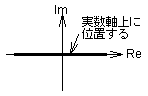図2-3-27	［過減衰］極は実数軸上に２点位置する．ζ>1の場合，極は虚軸より左（σ<0）に２点位置する．ζ<-1の場合，極は虚軸より右（σ>0）に２点位置する．

表2-3-4 極の位置と伝達関数の特徴２

２次系伝達関数の減衰比ζが発散・収束，振動などの特徴との関係は以前説明していました．ここで示した極の位置と伝達関数の特徴の関係から，次数の大きい伝達系にも対応することができます．

← 戻る 1 2 次へ →