20090608
ラプラス変換の質問
【20090530】質問
√t のラプラス変換はどうなるのでしょう?
√t のラプラス変換はどうなるのでしょう?
こちらに掲載しているラプラス変換表に,適合するものは無いので 定義から求めましょう.折角なので,ラプラス変換表に加えるべく tx という 形で導いてみたいと思います.
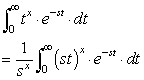 ---式1
---式1ここで,st を τ に置換して積分します.
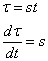
上式を代入して
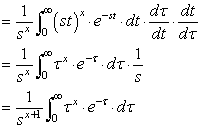 ---式2
---式2ここで
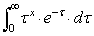 は,定数として収束します.ところでこの積分は,一般にガンマ関数として知られます.
一般的には次式のように定義されています.
は,定数として収束します.ところでこの積分は,一般にガンマ関数として知られます.
一般的には次式のように定義されています.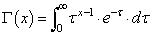 ただし x > 0
ただし x > 0ガンマ関数を導入して tx のラプラス変換を示すと
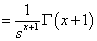 ---式3
---式3ガンマ関数は,一言で解説すると,階乗:n!=1×2×3×・・・×n の nを実数または複素数にまで拡張した 関数です. 工学の分野では,製品の経時劣化に関する信頼性/寿命の統計などの分野にも使用されます.我々の電子回路の分野では, パワー半導体などに関してワイブル等使って熱伸縮による金属疲労を解析したりといった分野に,なにげに多用されている関数です.
x が整数であれば,この積分はラプラス変換表の No.3に示した値と一致し,tnのラプラス変換は下記の通りです.
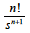
ガンマ関数を使って式3から展開すると √t のラプラス変換は,x=1/2より
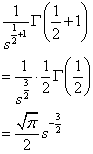
ガンマ関数の知識があれば容易ですが,一応ガンマ関数の知識が無くとも理解できるよう以下に進めます.
式2,x=1/2より
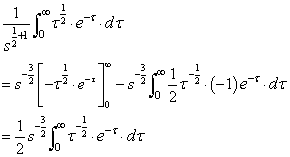
ここで置換積分
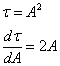
これを代入して
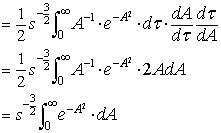
上式の定積分は,簡単そうに見えますが,意外に難しい積分です.ラプラス変換の主旨からは脱線しますので,ここでは割愛しますが, 上式を解くと先ほどのガンマ関数の答えと同様に得られます.
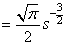
[記事URL] http://okawa-denshi.jp/blog/?th=2009060800
カテゴリー:質問と回答(13)
カテゴリー:質問と回答(13)
 前の記事
前の記事