20140731
PI補償器
PI補償器は,比例補償器と積分補償器を組み合わせた補償器で,それぞれの補償器の利点を活かしつつ 欠点を補う様に設計されます.
■比例補償器と積分補償器
まず,フィードバックの補償器に 比例補償器 および 積分補償器 だけを使った系を比較しながら,それぞれの特徴をおさらいしておこうと思います.比例補償器 および 積分補償器の詳細は,こちらを参照してください.→ 比例補償器によるフィードバック ,積分補償器によるフィードバック
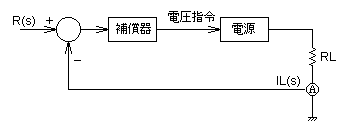
図1 フィードバック系
図1に示すフィードバック系を用いて,図中の補償器には 下表の制御図に記した比例器と積分器とを設置した場合の比較をします.
| 補償器 | 比例器 | 積分器 |
| 制御図 | 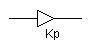 |
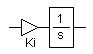 |
伝達関数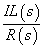 |
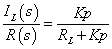 [計算過程] |
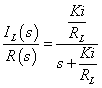 [計算過程] |
| ステップ応答 最終値 |
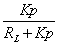 |
1 |
| ステップ応答 過渡 |
図2 青ライン | 図2 緑ライン |
| 特徴 | ○ 応答に遅れがない × 定常偏差がある |
× 応答遅れがある ○ 定常偏差が理論上0 |
表1 F/B補償器に比例補償器と積分補償器とを使った場合の比較
比例補償器だけを使ったフィードバックでは,定常偏差が0にならないことは ステップ応答最終値が1にならないことからわかります.次の図2ステップ過渡応答波形からも一目瞭然です. (比例補償器だけを使ったフィードバックの定常偏差についての記事はこちらを参照してください).
比例制御は,制御精度の面で十分とは言えない場合があります.しかし,比例ゲインを非常に大きくすれば,偏差は小さくなり,現実的な使用において ほとんど問題にならないように設定することも可能です(実際のアナログ回路では多く使われています).
[ステップ応答過渡]
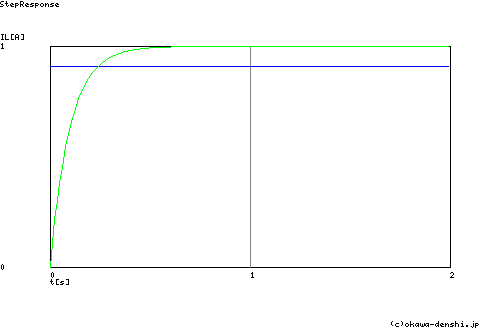
図2 比例器,積分器によるF/Bステップ応答
比例ゲイン:Kp=10
積分ゲイン:Ki=10
負荷抵抗:RL=1[Ω]
-: 比例補償器
-: 積分補償器
積分ゲイン:Ki=10
負荷抵抗:RL=1[Ω]
-: 比例補償器
-: 積分補償器
積分補償器だけを使ったフィードバックでは,利点として 定常偏差を理論上0にすることができます.(詳細は前回 解説しています). 一方欠点としては,比例制御では 指令R(s)入力から遅延なく制御量(電圧指令)が出力されますが,積分補償器のフィードバックでは,応答に遅延が生じてしまいます.図2のグラフからも読み取れます.
■PI補償器
遅延のない比例器と定常偏差が0の積分器の利点だけを活かし,両者の欠点を補うように補償器を設置できれば最良です.そのような意図から設計された補償器が,今回のテーマであるPI補償器です.
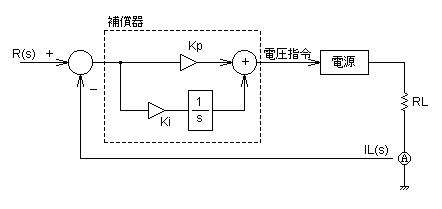
図3 PI補償器を使ったフィードバック系
図3は,図1のフィードバック系における補償器部分に,PI補償器を具体的に描き記しているものです.PI補償器は,簡単に言えば,前述の比例補償器と積分補償器のそれぞれに偏差を与え,両補償器の出力を重ねあわせた(足した)ものです.
PI補償器の部分だけを伝達関数にして示すと次式の通りになります.Kpは比例補償器の 比例ゲイン,Kiは積分補償器の 積分ゲインとします.
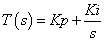
続いて,このPI補償器を用いた 図3の系の伝達関数
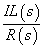 は次のように求めることができます.
は次のように求めることができます.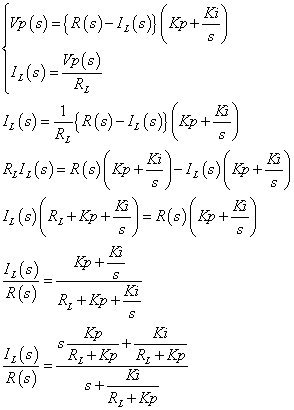
この伝達関数からこのフィードバック系の様々な特徴を見出すことができます.まず,STEP過渡応答から見て見ましょう. 伝達関数からSTEP過渡応答のグラフ,算出値のcsv(テキスト形式)を求めるWebアプリを用意していますのでご利用ください.
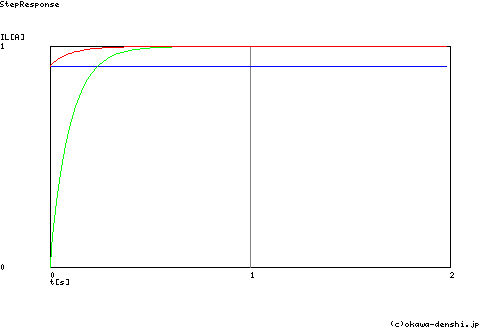
図4 PI補償器F/Bのステップ応答
比例ゲイン:Kp=10
積分ゲイン:Ki=110
負荷抵抗:RL=1[Ω]
-: 比例補償器
-: 積分補償器
-: PI補償器
積分ゲイン:Ki=110
負荷抵抗:RL=1[Ω]
-: 比例補償器
-: 積分補償器
-: PI補償器
補償器に 比例補償器,積分補償器 だけを使ったフィードバック系のステップ応答波形(図2のグラフと同じもの)にPI補償器を使ったフィードバックのSTEP応答波形(ライン赤)を併せて表示して比較しています.
ここで着目してほしい点は,t=0[s]において比例補償器と同等の制御量(電圧指令)が出力され,さらに,定常状態になってからは偏差がほとんど無いことが過渡波形から読み取れます.
初期値の定理と最終値の定理を使って,t=0[s]およびt=∞[s]におけるSTEP応答過渡値(過渡のIL[A])を求めることができます.
[初期値の定理]
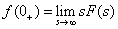
t=0[s]におけるIL[A]は,
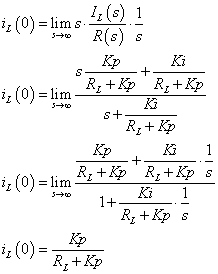
[最終値の定理]
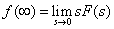
t=∞[s]におけるIL[A]は,
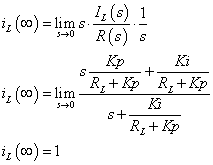
[初期値の定理]
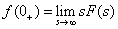
t=0[s]におけるIL[A]は,
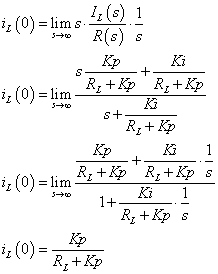
[最終値の定理]
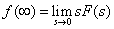
t=∞[s]におけるIL[A]は,
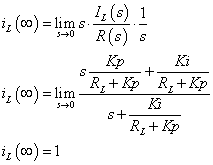
R(s)にステップ指令が与えられた瞬間に,比例補償器のフィードバック系と同等 遅延なく IL電流値が出力されます.さらに安定してくると,積分補償器のフィードバック系と同様に偏差が0に漸近していきます.
PI補償器によるフィードバックは,単純な構成でありながら,制御精度が高く,さらに応答性も良い,という優れた制御システムです. そのため,PI制御は非常に多くの分野で利用されています.
図3の系の伝達関数が,一般に次の式で与えられるとき
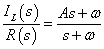
ωは特性周波数,Aはt=0[s]におけるILの瞬時電流となります.
ちょっと注意すべき点は,積分補償器だけを使ったフィードバック系の伝達関数のωと, PI制御 伝達関数のωとは数式が異なります. (例えば,P制御,I制御のそれぞれのゲインKpおよびKiが,PI制御のKp,Kiと同じ値に設定しても同じω(周波数特性)にはなりません.)
図4のPI制御のシミュレーションでは,ωが 積分補償器だけを使った系のωと同じ条件に設定しています.
[記事URL] http://okawa-denshi.jp/blog/?th=2014073100
カテゴリー:伝達関数ツール(15)
カテゴリー:伝達関数ツール(15)
 前の記事
前の記事