20140126
定常偏差と積分器
一般に電源などの定値制御を行う系では,目標値からの偏差(定常偏差)がなるべく 小さくなるように制御することが求められます. 今回の記事では,この定常偏差を小さくすることを目的とした 積分補償器 について考えていきます.
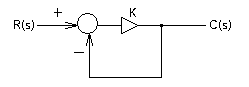
図1 比例制御の系
前回の記事で紹介した比例制御の系を簡単に示すと図1のようになります.この比例制御系の定常偏差は次式の通りです.この式の詳細は前回の記事で解説しています.
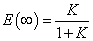 −−(1)
−−(1)出力C(s)は,Kの取る値(ただし K>0)によらず,基準R(s)よりも常に小さくなることが,式(1)からわかります(R(s)>0の場合).ここで,出力C(s)にoffsetを加えて 出力を調整できれば偏差を小さくできます.
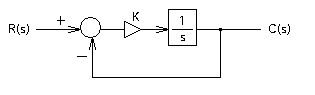
図2 積分補償器によるフィードバックの系
図2は,積分補償器によるフィードバックの系です.現実的な回路/システム設計で上図の系が設置されることはほとんど無いと思いますが,アナログ回路/制御設計における基本要素になりますので解説していきます.
積分器について
図1,図2のような図を制御図といいます.制御図にかかれるブロックは,数学的にすべて伝達関数に置き換えることができます.図2にかかれた は,特に積分器と言います.下図は,積分器に入力 A(s) ,出力 B(s) を設置したものです.
は,特に積分器と言います.下図は,積分器に入力 A(s) ,出力 B(s) を設置したものです.
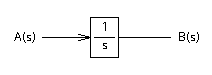
上図の系を,数学的に示すと積分器は伝達関数なので次のように示すことができます.
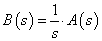
上式をラプラス逆変換して時間関数にして示すと
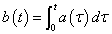
上式の通りです.伝達関数からもこの時間関数からも入力B(s)の時間積分が出力されます.(ラプラス変換表はこちらを参照してください.)
図1,図2のような図を制御図といいます.制御図にかかれるブロックは,数学的にすべて伝達関数に置き換えることができます.図2にかかれた
 は,特に積分器と言います.下図は,積分器に入力 A(s) ,出力 B(s) を設置したものです.
は,特に積分器と言います.下図は,積分器に入力 A(s) ,出力 B(s) を設置したものです.
上図の系を,数学的に示すと積分器は伝達関数なので次のように示すことができます.
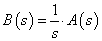
上式をラプラス逆変換して時間関数にして示すと
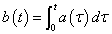
上式の通りです.伝達関数からもこの時間関数からも入力B(s)の時間積分が出力されます.(ラプラス変換表はこちらを参照してください.)
図2の積分器は,出力C(s)と基準R(s)の差(偏差)を時間で積分しています.その積分器の値(積分された値)が,系の出力,C(s)として出力され,その出力値と基準との差(偏差)が,再び積分器に入力されるフィードバック構成になります.
時間が経過すると,偏差が積分器により積分されることで,積分値が増加し(出力値も等しく大きくなり)ます.その結果,出力が基準に近づき偏差がゼロに近づいて行きます.
次に,図2の系を数学的に検証していきます.
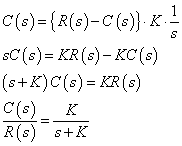 −−(2)
−−(2)式(2)は,系の入出力の関係を伝達関数によって示しています.
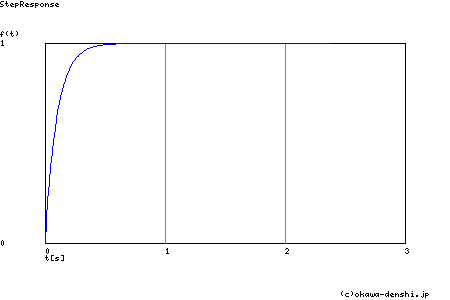
図3 積分補償器によるフィードバック系のステップ応答
K=10
図3は,式(2)の伝達関数のステップ応答の過渡波形です.この波形からも出力C(s)が基準R(s)に漸近していくことが読み取れると思います. ここでさらに,前回の記事でも触れた次に示す最終値の定理を使って,定常偏差の値を求めます.
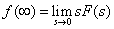 −−(3)
−−(3)式(2)(3)より,ステップ応答の最終値は
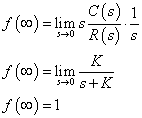 −−(4)
−−(4)ステップ応答の最終値はが,基準値と同じ1であることが確認できます.
現実のアナログ回路では,ゲインの上限は物理的な要因(仕様)により制限されます.そのため,この記事のような積分回路を設けた回路と,オープンゲインの回路とを比べた場合,定常偏差の大きさが変わることはありません. アナログ回路による制御で,積分器は 定常偏差の大きさの改善を目的とすることはほとんどありませんが,位相補償等の目的で用いられることが多いと思います.
ソフトウェアを用いたフィードバック系の場合には,この記事で記した積分器による定常偏差の設計は,PID制御などの要素として普通に組み込まれて使用されています.
[記事URL] http://okawa-denshi.jp/blog/?th=2014012600
カテゴリー:伝達関数ツール(15)
カテゴリー:伝達関数ツール(15)
 前の記事
前の記事