1.  前の記事
2. 次の記事 

フィルタを設計する上で多くの場合，指標にするのが周波数応答です．例えば，○Hzにおいて−□dBの利得といったような減衰の特性 を設計の目標とするような場合です．バターワースやチェビシェフ等といったフィルタ理論についても，周波数に対する減衰の効果を 設定するための理論になります．

しかし，現実にフィルタ回路を設計する場合，周波数応答だけの情報では思わぬアクシデントに見舞われるかもしれません． ここでは，一般的な周波数軸に対するゲインの応答だけでなく，実際に信号を入力した際の時間軸に対する過渡応答に着目して フィルタの特徴を様々な視点から捉えていきたいと思います．

---

■周波数特性でゲイン１倍を越える周波数が無くても振動する場合がある

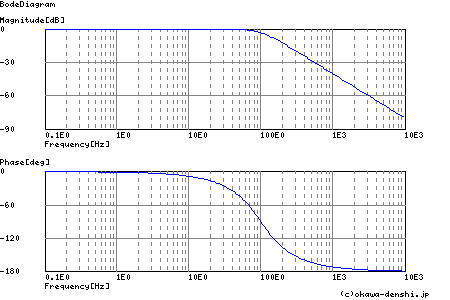
上図は，バターワース・フィルタの周波数特性（Bode線図）です．バターワース・フィルタの特徴として周波数応答のゲインが０ｄＢ（１倍） を越えません．よってこの周波数特性からは，利得１倍より大きい信号の増幅（振動成分）は無いように思えるかもしれません． しかし，STEP応答の過渡波形をみると．．．



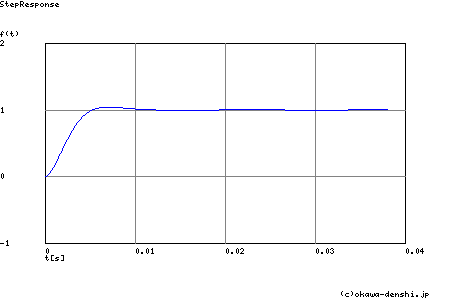
オーバーシュートを含む振動が有ることを読みとることができます．系の振動の有無は（バターワース・フィルタの）伝達関数における 減衰比の設定によります（→減衰比と振動の関係についての解説はこちら）．

例えば，２次バターワース・フィルタの伝達関数の減衰比は，

　　ζ ＝0.707

に設定しますので，ζ が１未満ということで系は振動するというわけです．

---

■非定常状態の過渡波形の挙動を知っておく

つづいて，入力波形が定常状態でない場合（常に周波数等変化している場合），多くのフィルタが必ずしも変化に即応して定常状態と 同様の波形を出力するものではありません．

下図のように，無信号の状態から振幅１の正弦波を与えた場合



過渡の例として，ζ ＝0.2 のバンドパスフィルタの応答を示すと



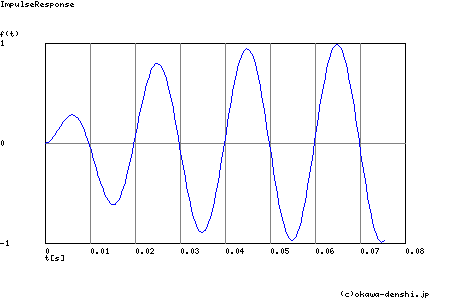
この波形の算出条件・方法はこちら．入力波形の変化の直後から，定常に おける信号の透過が100％得られている状態ではなく，徐々に定常へと推移することがわかると思います．

ここに示した例は，フィルタに対する信号変化の一例に過ぎませんが，一般にフィルタを用いた回路を設計する場合，定常状態ばかりを 扱うことは無いでしょうから，信号変化とその応答波形の関係をテストやシミュレーション等により把握して実機の設計を行うことが 必要です．