20150731
オペアンプを使ったPI補償器2
■前回の アナログ回路を使ったPI制御回路の例
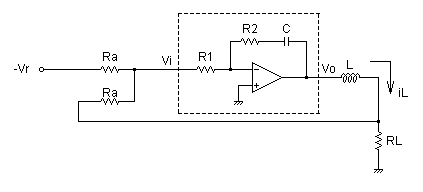
図1 PI補償回路を使ったLR直列回路の電流制御 例
図1の回路は,アナログ回路の制御をPI補償器をオペアンプを使って忠実に回路にしたもので,実際の回路設計では使われないと思います. 現実的なLR直列回路の電流制御は,こちらの記事非反転増幅回路を用いたLR直列回路の電流制御(後半)が参考になると思います.
図1の系の伝達関数は次の通りです.詳細は前回の記事(オペアンプを使ったPI補償器)を参照ください.
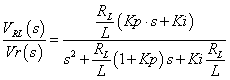 --- (1)
--- (1)ただし,Kp,Kiは
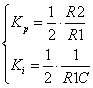 --- (2)
--- (2)■設計すべきパラメータは固定周波数ωと減衰比ζ
図1の回路は,式(1)の伝達関数から2次遅れの系であることがわかります.(n次遅れは伝達関数分母の複素数sの次数を示します.)
2次遅れの系について
2次遅れの系の場合,位相が最大で180degになりますので その場合のゲインによっては発振したり振動が大きくなったりします.
一般的な2次系の伝達関数を次式とします.
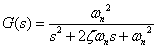 --- (3)
--- (3)
式(3)のωnは固定周波数,ζは減衰比といいます.
[減衰比ζについて]
次のグラフはζの値を振った,ステップ応答の過渡波形です.
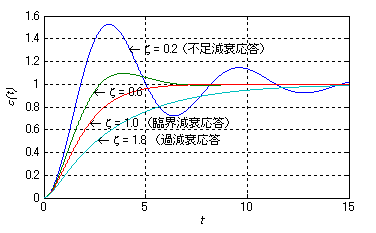 ωn=1
ωn=1
このグラフからも減衰比ζは振動を調整するパラメータであることがわかると思います.具体的には,ζ<1の条件で 系は振動します.
[固定周波数ωについて]
次のグラフは減衰比の値を固定してωの値を振った時の,ステップ応答の過渡波形です.
 ζ=1
ζ=1
− ωn=1
− ωn=2
− ωn=3
このグラフからも固定周波数ωは応答の速さを調整するパラメータであることがわかると思います.ζ<1の条件では,系の振動周波数に関係します.
2次遅れの系の場合,位相が最大で180degになりますので その場合のゲインによっては発振したり振動が大きくなったりします.
一般的な2次系の伝達関数を次式とします.
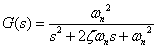 --- (3)
--- (3)式(3)のωnは固定周波数,ζは減衰比といいます.
[減衰比ζについて]
次のグラフはζの値を振った,ステップ応答の過渡波形です.
 ωn=1
ωn=1このグラフからも減衰比ζは振動を調整するパラメータであることがわかると思います.具体的には,ζ<1の条件で 系は振動します.
[固定周波数ωについて]
次のグラフは減衰比の値を固定してωの値を振った時の,ステップ応答の過渡波形です.
 ζ=1
ζ=1− ωn=1
− ωn=2
− ωn=3
このグラフからも固定周波数ωは応答の速さを調整するパラメータであることがわかると思います.ζ<1の条件では,系の振動周波数に関係します.
図1のような2次伝達関数で表せる系の場合,制御部分で設計すべきポイントは,数学的には固定周波数ωと減衰比ζの2パラメータの設定に限定することが可能です.
そこで,(1)式の伝達関数から固定周波数ωと減衰比ζを算出しましょう.(1)(3)式より
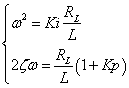
上式より
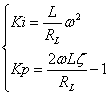 --- (4)
--- (4)まず,減衰比ζの設定について,推奨される設定値は次の通りです.
ζ=1 --- (5)
ζ>1に設定すると緩慢な応答になり,ζ<1に設定すると系が振動します.ζ<1では,極端な場合には 不安定になったり振動によって異音が発生する場合もあります.減衰比ζの設定において,系が振動せず最も応答の速い値が,推奨値のζ=1です.
系の応答の速さを調整するパラメータは,固定周波数ωです.ωを大きくするほど系の応答は速くなります.ただし,(1)式の伝達関数の場合,分子にs項がありますので,ζ=1の条件でも ωを大きくしすぎるとオーバーシュートが出ます.
オーバーシュートを許容しない仕様で際限なく応答を速くしたい場合は,別の回路を考える必要があります.その際はこちらの記事非反転増幅回路を用いたLR直列回路の電流制御(後半)を参照してください.
■パラメータ設計の例
オーバーシュートが発生する場合,過渡であってもハードウェアの耐出力電流を大きく設計しなければならない場合もあります.そのような要因により機器が大型化しないように,制御部については オーバーシュートを許容しない仕様としている機器も多いと思います.そこで この記事でのパラメータ設計例では,オーバーシュートを許容しない条件で調整をしてみたいと思います.
ハードウェアの仕様
RL=0.1Ω --- (6)
L=100μH --- (7)
制御上の設定
ζ=1 --- (8)
ω=1000rad/s --- (9)
RL=0.1Ω --- (6)
L=100μH --- (7)
制御上の設定
ζ=1 --- (8)
ω=1000rad/s --- (9)
(9)式のωの設定について
まず,(1)式の伝達関数をωの関数として表します.(1)(4)(8)式より
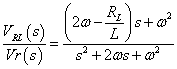 --- (10)
--- (10)(10)式について伝達関数計算ツール等ツールを使って,ωを振りつつオーバーシュートを確認します.少し余裕ありますがここでは,(9)式の通りω=1000rad/sに設定します.
(6)〜(9)式の条件で,Ki,Kp,R1,R2,Cを計算すると次式の通りになります.
Ki=1000 --- (11)
Kp=1 --- (12)
(2)式より
R1=5KΩ(5.1KΩ) --- (13)
R2=10KΩ --- (14)
C=0.1μF --- (15)
■参考までにSPICEによるシミュレーション
回路パラメータの具体設定は,次の回路図中に表していますので参照してください.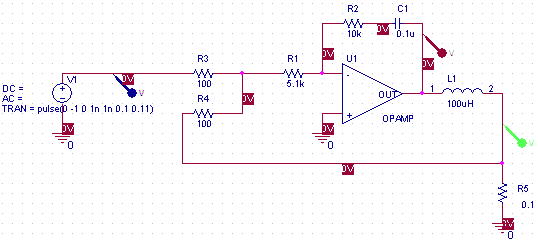
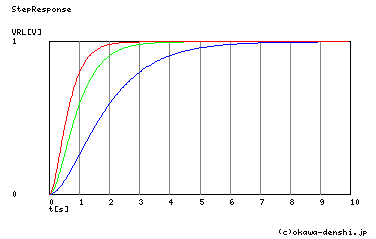
次のグラフは,step応答の過渡波形をSPICEによってシミュレーションしたものです.上図のプローブの色が下図グラフの波形色に対応しています.
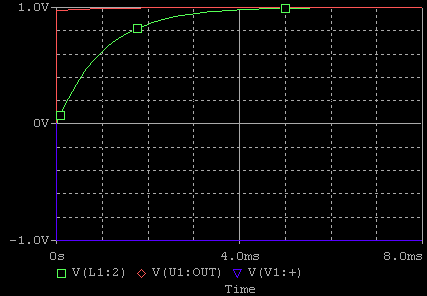
この記事では,回路上の公差/温度ドリフトなどは考慮していませんが,実機の設計においては考慮が必要です.
[記事URL] http://okawa-denshi.jp/blog/?th=2015073100
カテゴリー:伝達関数ツール(15)
カテゴリー:伝達関数ツール(15)
 前の記事
前の記事