1.  前の記事
2. 次の記事 

”アナログ回路の設計で伝達関数を利用する”という切り口で，前回は，LR直列回路の電流制御における立ち上がり時間の調整 （パラメータの設定によって応答の速さを自在に調整する内容）について書きました．

今回の記事も同様に，LR直列回路の電流制御における定常偏差について伝達関数を利用しながら考えてみましょう．

■一般的なフィードバック系と定常偏差

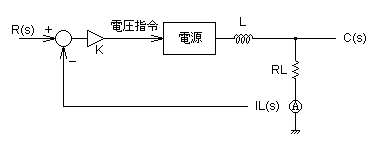
図3 LR回路の電流制御系

図３は，LR直列回路に電源（電圧源）を接続した回路で，電源の電圧を調整することでLR回路の電流を制御する系です．フィードバック系としては 一般的で，制御工学の教科書などでもよく用いられる系です．

しかし，オペアンプを使用したアナログ回路では，このフィードバックの系とは異なる場合があります．アナログ回路特有の制御系については， この記事の後半で紹介します．

まずは，図３の系の伝達関数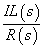を求めてみましょう．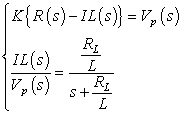

    
Vpは電源の出力電圧．
上式から伝達関数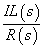は，次式の通り．
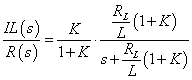            −−(3)
        (途中式はこちら)．

---

伝達関数(3)式から定常偏差を考えます．最初にステップ応答を確認しておきましょう．

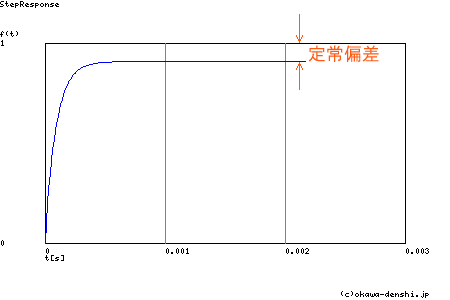
図4 LR回路制御系のステップ応答

条件：
  L＝1[mH]
  RL＝1[Ω]
  K＝10

図４は，K=10における制御系のステップ応答例です．この応答から定常偏差についてざっくりとした値ですが見て取ることができます．ステップ応答ですので 入力指令Rは，１[A]です．それに対して定常状態の出力ILは，およそ0.9[A]といったところでしょうか．指令と結果には差（偏差）が生じていることが 図から読み取れると思います．

ここで，この定常偏差を定量的に求めるためには，ステップ応答におけるt=∞[s]時の過渡関数の値を求める必要があります． 最終値の定理という便利な方法がありますので 利用していきます．詳細はこちらを参照してください．

最終値の定理は，式(4)の関係によって示すことができます．

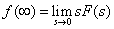            −−(4)

上式のF(s)は，システムの応答を示す関数です．f(∞)は，時間を引数とする過渡関数f(t)のt=∞における値（最終値）を示します． 制御系の定常偏差は，系にステップ指令を入力した際，t=∞[s]の 偏差になります．

そこで，(4)式を使って伝達関数(3)式のステップ応答最終値を具体的に求めてみましょう． (4)式内のF(s)は，図３の系の場合にはIL(s)になります．

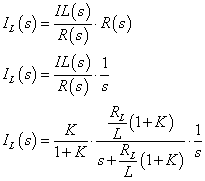            −−(5)

式(5)を最終値の定理を使ってiL(∞)最終値を求めていきます．

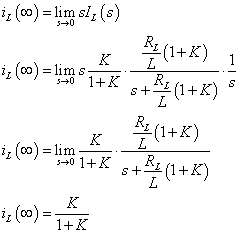            −−(6)

式(6)からわかることは，定常偏差は比例ゲインKの関数になっていることがわかります．Kの値が大きいほど定常偏差は小さく，Kの値が小さいほど定常偏差は大きく なります．

図４のステップ応答最終値は，K=10のシミュレーションではおよそ0.909…[A]であることが式(6)より求められます．よって定常偏差e(∞)は，指令値rが1[A]であることから およそ0.091[A]になります．

---

■非反転増幅回路を用いたフィードバック系と定常偏差

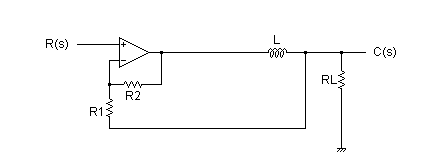
図2 LR直列回路の電流制御系

先ほど取り上げた図３の系のような，LR直列回路の電流制御をアナログ回路を使って設計する際の一例として，図２に示しました． この図２の系は，前回の記事でも扱ったフィードバック系です．

この回路についても，先ほどと同様 最終値の定理を使って定常偏差を求めてみましょう．まずこの系の伝達関数は次式の通りでした．（この伝達関数についての詳細は 前回の記事を参照してください）．

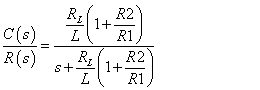            −−(1)

式(3)のKをR2/R1に置き換えると式(1)と似たような式にはなります．共通点としては，制御周波数 ωが同じ点です．

この系についても先ほどと同様にステップ指令を与えた際の定常偏差を求めていきます．

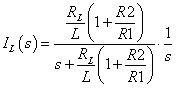            −−(7)

式(7)はステップ指令を与えたときの応答関数です．式(7)を最終値の定理によってiL(∞)最終値を求めていきます．

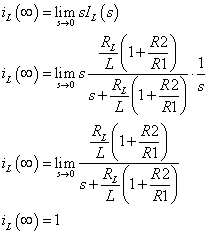            −−(8)

式(8)から言えることは，R1，R2 などのパラメータの値によらず最終値は常に1[A]になるということです． そのため，定常偏差e(∞)は，指令値rが1[A]ですので常に0[A]になります．

（ちなみに，現実の電子回路では電子部品の特性や公差により制御誤差が，0[A]になるわけではありません．）

一応 前回シミュレーションしたステップ応答の波形を参考までに掲載しておきます．


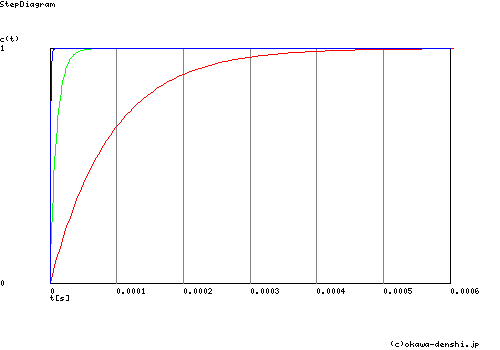
条件：

---

図３のフィードバック系と図２の非反転増幅の系の違いを，それぞれ伝達関数から数学的に抽出すると，定常偏差が違う（伝達関数の係数が異なる）という ことになります．

制御構造の観点から，前者の制御系と後者の制御系の相違点は．

        非反転増幅回路 ≠ 偏差の増幅

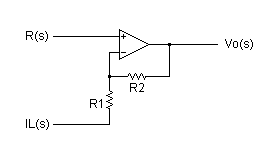
図５ 非反転増幅回路

図５の入出力の関係を数式で表すと次式の通りです．

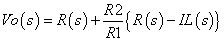            −−(9)

図５の非反転増幅回路では，R(s)-IL(s)の偏差の R2/R1 倍した値に R(s)を加えたものが Vo として出力されます．式(9)から分かる前者との相違点は， R(s)を加えている点です．

ちなみに式(9)の関係を制御図で示すと下図のようになります．

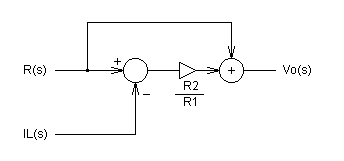
図６ 非反転増幅回路の制御図

R(s)の加算部だけを抽出して回路に示すと，図７のようになります．

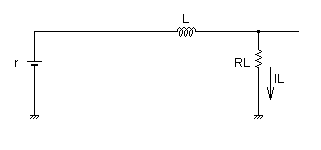
図７ 直流電圧の重畳

図３の制御系に，図７に示す直流電圧が重畳していると考えればわかりやすいと思います．

後者の系は，指令値とILが完全に比例関係にあるので定常偏差をきっちり0[A]に設定できますが，PWM駆動の電源等を介してデューティ指示に変換されれば， 固定のデューティが重畳されますがILと必ずしも比例関係になるとは限りませんので，定常偏差は0[A]ということにはなりません．

図２の制御系の場合，定常状態における指令値（図７のr電圧）とRLに印可される電圧が一致するように意図的に設計したことにより定常偏差を0[A]に設定できます．

この系のように指令値に目標となる値を重畳させることにより，低いフィードバックゲインでも定常偏差を低く設計することができます． このような方法は，アナログ回路に限らずデジタル制御においても全く同様に実現することが可能です．

---

前者の制御系は比例ゲインによるフィードバックで， このあたりの制御が起点となって学問分野や産業分野など多岐多様に展開されています．

この記事で取り上げた２例の制御系から，定常偏差を比較することで非反転増幅回路を伝達関数として数学的に特徴を捉えることができたと思います． この記事では，制御における非反転増幅回路のメリットとして扱いましたが，逆に扱いにくい場合も多々あります．

どちらにしても系を数学モデル化することによって挙動を正しく捉えることができます．また，数学的な解を得ることで，パラメータ設定が容易になり さらに設計の根拠も明確になるメリットがあります．