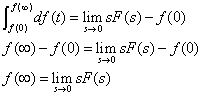初期値,最終値の定理
フィードバックを用いた制御システムなどで,過渡現象における最終値を知ることができれば,基準(指令値)と最終値を比較することによって理論的な静的制御偏差を得ることができます.
これまで過渡現象の最終値を知るためにはラプラス関数から過渡関数を求めた上で t=∞[s]の極限から得る方法が可能です.
しかしこのセクションでは,もうちょっと簡単な方法で,ラプラス関数のまま,最終値を得られる最終値の定理について説明します.また,最終値の定理と対となる初期値の定理があり,これは過渡現象における初期値(t=0[s]における極限値)に関する定理です.併せて説明していきます.
| 初期値の定理 | |
式2-3-28 |
| 最終値の定理 | 式2-3-29 |
初期値定理の説明
式2-3-28について説明します.まず,ラプラス変換表(表2-1-4)No.5の導関数のラプラス変換から
| No | 時間関数 f(t) | ラプラス関数 F(s) |
| 5 | f '(t) | sF(s)-f(0) |
上表の変換をラプラス積分を用いて示すと
![]()
より
![]()
ここで s→∞の極限値を考えると
![]()
ここで
![]()
なので
![]()
最終値定理の説明
式2-3-29について.初期値定理の説明と同様に,導関数のラプラス変換より
![]()
より s→0の極限値を考えます.
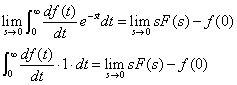
ここで左辺のtによる積分を,dt/dtを約分してf(t)による積分に変換すると(応じて積分範囲も)