ラプラス逆変換

このセクションではラプラス逆変換について説明します．ラプラス逆変換はラプラス変換とは逆に複素数sの領域の関数を時間tの領域の関数に変換する数学的手法です．

電子回路の過渡現象などの微分方程式を解く際，ラプラス逆変換はラプラス変換と対で利用されます．これまでラプラス変換についてラプラス積分を解くことによってラプラス変換してきました．しかしラプラス変換をする際，ラプラス変換表を使って変換する方法が一般的です．

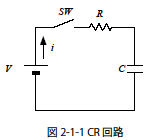
これと同様にラプラス逆変換についてもラプラス変換表を用いて変換する方法が一般的です．そこで先に述べたCR回路の過渡現象の回路例（右図2-1-1）にてラプラス逆変換を使って解いてみます．

この回路における電圧，電流の関係は式2-1-2のようになります．（詳細はこちら）

まずこの式を両辺ラプラス変換すると

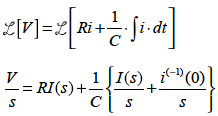
i^(-1)(0) はt=0 におけるコンデンサの充電電荷なのでq(0) とします．ここからI(s)について代数的に解いていきます．

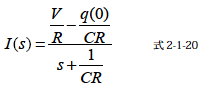
次にこの式のようなsの関数をラプラス逆変換します．方法はsの関数（式2-1-20）をラプラス変換表（表2-1-3，表2-1-4）の型に合うよう変形し表を参照しラプラス逆変換します．式2-1-20の場合表2-1-3の４にあてはめて変換すると

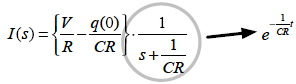
よって

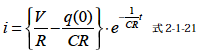
と解くことができました．ただし，t=0[s] におけるコンデンサの充電電荷が0[C]であるとするとq(0)=0 なので電流i は

と解くことができます．