20160131
制御の安定
前の記事- 次の記事
一般にフィードバック回路の設計において求められる安定性とは，時間経過とともに過渡応答が０に収束して定常的な状態になることを安定と言います．不安定な系では，時間経過とともに過渡の応答が増大します．制御システムを設計する上で，どのような条件であっても系を安定化する必要があります．
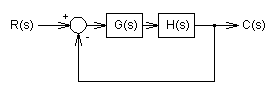
図1 一般的なフィードバック系
この系の閉ループ伝達関数は次の通りです．
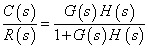--- 式(1)ちなみに，閉ループ，開ループとは下表の通り．
| 閉ループ | 上図のように帰還のかかっている系 |
| 開ループ |  上図のように帰還のかかっていない系 |
■正帰還とシステムの状態
安定性についてわかりやすく理解するために次のようなフィードバック系を考えることにします．
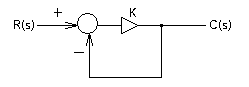
図2 一般的なフィードバック系
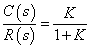--- 式(2)| Kの範囲 | 帰還 | 安定性 | 備考 |
| K＞0 | 負帰還 | 安定 | 通常の負帰還で常に定常状態（安定）． |
| K＝0 | - | 安定 | 零点，常に出力が0の定常状態で安定． |
| -1＜K＜0 | 正帰還 | 安定 | Kの値が負なので結果的に正帰還のようなシステムになる．このKの範囲で定値制御はできない．過渡の応答は増大しないので一応安定．下記シミュレーション参照 |
| K≦-1 | 正帰還 | 不安定 | Kの値が負なので結果的に正帰還のようなシステム．過渡の応答が増大するので不安定．この条件では，式(2)を適用できません． |
-1＜K＜0の範囲が安定？
Kが，-1＜K＜0の範囲では実質的に正帰還となりますが，系は安定状態になります．具体例を示すので考えてみてください．K=-0.5
R(s)=1
の条件では，式(2)より
C(s)=-1
図２の制御図上の各値（引き出し線の値）を算出します．
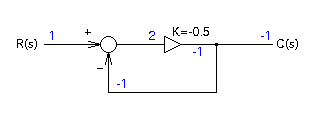
図3 安定している正帰還の例
図３の青文字で示す通り値が矛盾なく定まります．ちょっと不思議な感じもすると思いますが，このように定常的に値が固定し過渡的な変化がありませんので安定と言えます．
ただ，安定であれば問題が全くないかといえば，そうではありません．制御上の偏差は大きく定値制御できているとは言えません．正帰還の系が存在しないわけではありませんが，用途は限られています．
まとめると，制御系のフィードバックが結果的に正帰還になる場合，その帰還ゲインが１倍以上になるとその系は不安定になります．設計上注意するポイントとしては，どのような条件下であっても常に -1＜K に設定することが必要です．
続く