20090607
システムの線形とラプラス変換
前の記事
【20090504】質問
E= L*∫i(t)dt +R*(1+sin ωt)*i(t) の様な場合、
E/s= L*s*i(s) +R*i(s) +R/2j*( i(s-jω)-i(s+jω) )
となりますが、逆変換のための i(s) は、どうすれば求まるでしょうか？
【20090513】追加
１週間ほど前、下記のご質問をする際、Ｌ＊∫i(t)dt となっていたかも知れません。L*di(t)/dt の間違いです。すみません。
E= L*di(t)/dt +R*(1+sin ωt)*i(t) の様な場合、
E/s= L*s*i(s) +R*i(s) +R/2j*( i(s-jω)-i(s+jω) )
となりますが、逆変換のための i(s) は、どうすれば求まるでしょうか？
E= L*∫i(t)dt +R*(1+sin ωt)*i(t) の様な場合、
E/s= L*s*i(s) +R*i(s) +R/2j*( i(s-jω)-i(s+jω) )
となりますが、逆変換のための i(s) は、どうすれば求まるでしょうか？
【20090513】追加
１週間ほど前、下記のご質問をする際、Ｌ＊∫i(t)dt となっていたかも知れません。L*di(t)/dt の間違いです。すみません。
E= L*di(t)/dt +R*(1+sin ωt)*i(t) の様な場合、
E/s= L*s*i(s) +R*i(s) +R/2j*( i(s-jω)-i(s+jω) )
となりますが、逆変換のための i(s) は、どうすれば求まるでしょうか？
まず，はじめに物理解を得るためには，回路図や，力学の系だとか背景となる情報が最低限必要です． 提供する情報が少なければ，アドバイスできる範囲が小さくなり，質問者の得たい情報が得にくくなってしまいます．
質問の出発点である
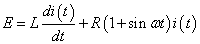--- 式１は，ラプラス変換可能なシステムを対象としていない可能性があります．この式が導き出されるまでの過程がわからないので， 断定はできませんが．
もし，解があることが確定しているラプラス変換に関する練習問題や課題について質問しているのなら，式１は間違っていると考えます．
ところで，ラプラス変換可能なシステムは，線形システムです．ラプラス変換に限らず，すべての物理現象は線形性の保たれた空間で展開されて います．
線形性の保たれた空間とは，一言で言えば重ね合わせの理が 適用できる空間です．たとえば，ある空間に電荷ΔＱが現れたとき空間に与える電界の変化ΔＥは，いかなる直前の空間の状態によらず 一定不変ということです．
式１の数式から背景となるシステムを勝手に推測すると次のようなＬＲの直列系があったのかと考えます．
 |
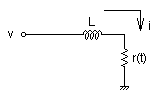r(t) = R(1+sin ωt) v = E |
抵抗r(t)が時間とともに変化するというところが，この系の特徴でしょう．
ここでこの系が非線形であることを説明するために，vにあたえる電圧を次のように階段状に与えた場合を考えます．
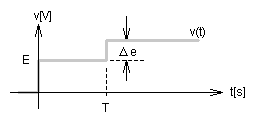
Eのステップ応答によるi(t)が流れる状態に加えて，vのΔe の変化を与えた際のi(t)の変化量をΔiとします．
線形システムであれば，Δe＝E であれば 電流の変化量Δiは，Eのステップ応答による電流と波形が完全に一致します．しかし， 上系においては，時間とともに r が変化するため 時間T の大きさにより変化量Δiの波形は異なります．よって簡単ではありますけど 上系が非線形であることがわかると思います．
ご質問の結論としては，ラプラス変換およびラプラス逆変換はできないということになります．