回路網の計算2 〜重ね合わせの理〜
回路網計算に使われる重ね合わせの理を説明します.この法則は回路網計算だけでなく場や空間にも適用される広義の物理法則としても知られています.
重ね合わせの理という名前の通り,複数の電荷がつくる電界や複数の微小電流がつくる磁界などは,それぞれの電荷や微小電流など単体がつくる場の重ね合わせ(ベクトル和)によって合成されます.回路網計算で使われる重ね合わせの理は電荷のつくる電界の重ね合わせの応用として利用されます.
重ね合わせの理 (電荷と電界)
複数の電荷によってつくられる電界は,空間に存在する電荷一個一個がつくる電界のベクトル和によって求められます.ある電荷のつくる電界を考えるときその他の電荷は0[C] と仮定します.重ね合わせの理によってある電荷の存在によって空間に与える電界の影響について簡単に求めることができます.
つづいて重ね合わせの理を複数の電源と抵抗からなる回路網計算への応用を考えます.通常の回路内では1次元〜2次元未満の要素として簡易的に考えることができますのでベクトル和を電流のプラス,マイナスを意識しつつ単純に足しあわせることで実現できます.
重ね合わせの理
複数の電源と抵抗から構成される回路網において,回路網中の任意の電流は個々の電源が回路網全体に与える電流の和になります.ある電源の与える電流を考えるとき回路網を構成するその他の電源を0Vと仮定します.
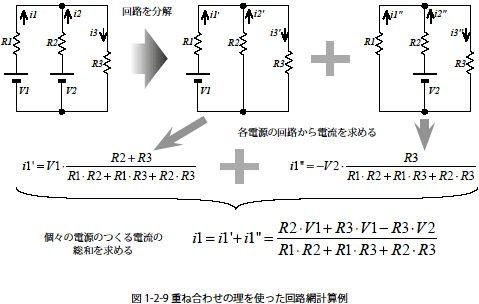
具体的にはキルヒホッフの法則で解いた図1-2-7 の回路例について,再度重ね合わせの理を使ってi1 を求めてみます.考え方は図1-2-7 の回路を図1-2-9 のようにそれぞれの電源の影響による電流を求めるため各電源ごとの回路に分割します.その後分割して求めた各ポイントの電流を足し合わせて回路網における電流を求めます.
複数の電源と抵抗から構成される回路網において,ダイオードが入った回路でも重ね合わせの理で計算できるのでしょうか?計算例を教えてください。
【回答】2008/06/20
ダイオードのIF-VF特性は,ご存知のように指数(Exponential)関数で与えられます.一般式は下記の通りです.
| IF =IS(AbVF-1) | 式3-2-5 | VF[V]:順方向バイアス IS[A]:飽和逆方向電流 A[ ]:固定定数 b[V-1]:温度に係わる係数 |
VFが0Vの場合,IFも0Aとなり,原点を通るところは理論抵抗と同様ですが,ダイオードの場合与えるVFによってダイオードの抵抗値が変化します.この点が唯一理論抵抗と異なる点です.ダイオードの抵抗値は,式3-2-5より
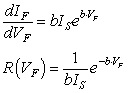 |
式3-3-7 式3-3-7 |
A=eとして
|
ダイオードに限りませんが,抵抗器として入手できる電子部品も理論抵抗とは異なるものですので,ご質問の件と大きな視点で捉えれば同じ問題なのです.
要するに,回路網にある条件を与えたときにその電子部品は何Ωかということが問われ,真の抵抗値が与えられれば,オームの法則,キルヒホッフの法則,重ねの理など抵抗計算に関するすべての法則に従うことになります.工業製品においては,ダイオードなり抵抗なりの理論抵抗真値がどの程度の変動があるのかを設計に織り込む訳です.
「計算例を教えてください」ということですが,ずいぶん漠然としてるので,上の図1-2-9についてR1,R2,R3のいずれかをダイオードによる抵抗と読み換えてもいいんですが...,もし抱えている問題があるのでしたら具体的に回路等の条件を呈示していただいた方が答えやすい.ダイオード+内部抵抗の計算例はこちら(重ねの理は使いませんがオームの法則くらいは使います)