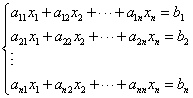回路網の計算１ 〜キルヒホッフの法則〜
回路の分岐が多くなったり電源が複数に増えたときも，分岐した電流やそれぞれの部品にかかる電圧は，基本的にはすべてオームの法則に従います．ここでは回路網の複雑な計算を便利に解く法則について説明していきます．まず最初に回路網計算の定番のキルヒホッフの法則 を説明します．キルヒホッフの法則は第一法則と第二法則とで構成されています．
キルヒホッフの第一法則
回路網上の任意の電流の分岐点において電流の流入の和と流出の和は等しい．
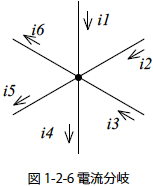
図1-2-6 の場合では，i1 〜 i3 は分岐点に流入する電流でi4 〜 i6 は分岐点から流出する電流なので
i1+i2+i3=i4+i5+i6
の関係があります．
キルヒホッフの第二法則
回路網上で任意の閉じた環状の電路をたどるとき電路中の電源の電圧の総和と電圧降下の総和は等しい．
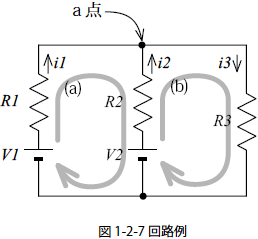
図1-2-7 の回路例について
の電路(a)，(b) をキルヒホッフの第二法則を用いて示します．
V1-V2=R1・i1-R2・i2 (a)
V2=R2・i2+R3・i3 (b)
となります．上式は左辺を電源電圧の総和として，右辺を電圧降下の総和として示しています．
電源および電圧降下の総和は，任意の環状電路を選択してその電路について電圧極性の方向を任意に決めます．たとえば電路(a) の場合，V1 の電圧の方向（極性）を正と決めるとV2 は負となります．よって電源電圧の総和はV1-V2 となります．次に，抵抗の電圧降下を求めるとき，まず回路の各部（各抵抗）に流れる電流をi1 〜 i3 のように置いて電流の向きを仮に決めます．電路(a) の方向に流れる電流を正とすればi1 が正，i2 が負となり，それぞれの電圧降下はR1・i1，-R2・i2 となります．
このようにして第一法則と第二法則から連立方程式をたてます．数学的に連立方程式によって解を求める場合，方程式の数は求めたい未知数の数と同数必要となります．図1-2-7 の回路例で求めたいパラメータはi1，i2，i3 なので未知数の数は３となります．そのため方程式は３本必要です．
こうして連立方程式を解くと，求めたパラメータがマイナスの値になることがあります．この場合，最初に仮に決めたパラメータの極性が反対であったことになります．
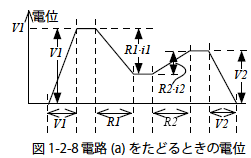
図1-2-8 は電路(a) についてV1 のマイナス端子からに沿って電位を示しています．環状にたどっているので出発点と終点は回路上の同じ場所となります．
そのため当然ですが出発点と終点の電位は同じになります．このことから考えても回路網の任意の環状電路において，出発点と終点の電位が同じため電源電圧の総和と電圧降下の総和は等しくなります．
(1)図1-2-7の各電流について
図1-2-7 の回路についてキルヒホッフの法則を使ってi1 〜 i3 を求めてみましょう．まず第一法則からａ点における電流の流入の和と流出の和の関係は
i1+i2=i3
となります．続いて第二法則より環状電路(a)，(b) について電源電圧の総和と電圧降下の総和の関係を求めます．
これら３式からなる連立方程式よりi1 〜 i3 を解くとつぎのようになります．
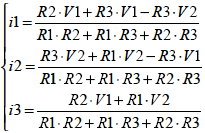
キルヒホッフ第１の法則より、
ｌ１＝２A、ｌ２＝３A、ｌ３＝４で他に電流の逃げが無い場合も０になるのでしょうか？
【回答】2008/04/02
電流は水の流れにたとえられることが多く，この場合も例に漏れず水流をイメージするとわかりやすいと思います．
ご質問では，I1〜I3の３本の電路がＹ字状に結線されているものとして， これを水流にたとえると，水道管のようなパイプが３本Ｙ字状に結合されているところをイメージしてください．
上流から下流２本へ分流しても，上流２本から下流１本へ合流しても，Ｙ字の結合点における流れ込みと流れだしが同じ水量になることがイメージできると思います． これは，Ｙ字の結合点やその他の水路に水漏れが無いことを条件としているためです．
電流においても同様で，電路および結線部の電流漏れが無い場合，電流の流れ込みと流れだしが同じ電流値になります．
ご質問のｌ１＝２A、ｌ２＝３A、ｌ３＝４Aという条件は，現実的にはつくりだすことはできません． キルヒホッフ第１の法則ではｌ１＝２A、ｌ２＝３A、とすれば，ｌ３＝−５Aということになります．
【質問】2008/04/13
１．すべての電流の向きがa点に流入する回路ってあるんですか？
２．
-I1=I2+I3
V1=R1I1-R2I2
V2=R3I3-R2I2 の時
i1 i2 i3はどうなりますか？
【回答】2008/04/13
１．について
前質問と同様で，水道管のようなパイプが３本Ｙ字状にa点に結合されているところをイメージしてください． a点に漏れや膨らむような構造でない限り，一点に水は流れ込まないことが想像できると思います．電流も同様です． よってご質問の，すべての電流の向きがa点に流入する回路はありません．ただし次のようにすべての電流の向きがa点に流入する条件設定することがあります．
a点
i1→・←i2
↑
i3
このような設定の場合，仮にi1が正の値をとれば，i2またはi3が負の値をとります．流入の合計が0A（i1+i2+i3=0）となります．
２．について
回路図がこちらで想像できませんので，再度回路図を含めて投稿ください．
