回路網の計算3 〜鳳テブナンの法則〜
鳳- テブナンの定理は複数の電源と抵抗から構成される複雑な回路網をシンプルな回路モデル(電源と抵抗の直列に接続した回路)に等価変換するための定理です.
鳳-テブナンの定理
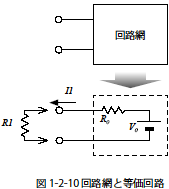
複数の電源と抵抗から構成される回路網において,回路網中の任意の2点を外部からみたとき,その回路網は電源V0 と内部抵抗R0 が直列に接続された回路に等価して扱うことができます.この等価回路はオームの法則などの物理法則にも従います.
この2点に抵抗R1 を接続したときR1 に流れる電流I は次のようになります.
![]()
等価回路中のV0 は2点間をオープンにしたときの電圧です.また,R0 は回路網中のすべての電源を短絡状態と仮想して2点端からみた抵抗値です.
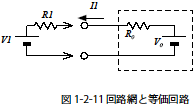
鳳- テブナンの法則によって回路網中の任意の2点を外部からみたときの,仮想的につくられた電源(V0)と内部抵抗(R0)の直列回路に,電源と抵抗を接続したときも同様に電流を求めることができます.図1-2-11 は回路網の等価回路に電源V1 と抵抗R1 を接続した図です.
![]()
この鳳- テブナンの定理によって複数の抵抗と電源で構成される回路網に部品や電子回路を挿入する際の計算を簡単に行うことができます.
(1)鳳-テブナンの定理についての解説
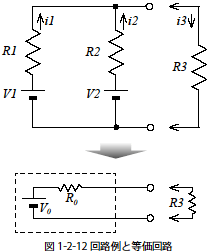
図1-2-7 の回路例で鳳- テブナンの定理を使ってi3 を求めてみます.図1-2-12 に示すようにR3 を回路例から切り離した系を想定し考えてみます.
まず最初に,図1-2-12 のV1,V2,R1,R2 から構成される回路をV0,R0 からなる等価回路に変換します.
つぎにV0 を求めます.V0 は2点間をオープン(開放)にしたときの電圧なので
![]()
となります.
つぎにR0 を求めます.R0 は回路網中のすべての電源を短絡として仮定した状態の回路によって,R3 の接続される2点間からみた抵抗値(R1とR2の並列接続の系)となるので式1-2-18 となります.
![]()
i3 は鳳- テブナンの定理より,つぎのようになります.
![]()
よって式1-2-17,式1-2-18,式1-2-19 よりi3 は
![]()
となります.
電源が3つある時はどういうほうほうで求めたらいいのですか。
【回答】2008/07/24
ある2点間から見た電子回路Aが,複数の抵抗と複数の電源から構成される場合,一本の等価抵抗とひとつの電源が直列に接続された系 として電子回路Aを等価的に扱うことができます.その考え方は,電源が3つあっても考え方は一緒です.
さて,ご質問の電源が3つある場合ということですがこちらで回路が推測できません,恐れ入りますが回路,その他情報を含めて投稿して ください.また,ご自身で課題を解き,間違っていてもかまわないのでその道筋を示していただくと適切なアドバイスができると思います.
仮に複雑な系でも,簡単な系に分解して複数回 テブナンの定理や重ね合わせの理などを応用すると比較的簡単に導くことができますよ.