ダイオードの静特性

ダイオードに順方向バイアス V_Fを与えたときに，ダイオードに流れる電流 I_Fとの関係を考えます．一般に市販されるダイオードは次に示す特性を持ちます．

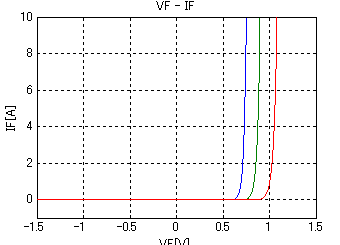
図3-2-31 ダイオードの VF-IF 特性

ダイオードに流れる電流は，ＰＮ接合部に存在するキャリア（電子とホール）の電荷量に応じて調整されます．バイアスが与えられない状態では，ＰＮ接合部は空乏層となっておりキャリアはほとんど存在しません．しかし，外部から（順方向）バイアスを与えることによって，電子やホールが障壁を越え移動することによって接合部のキャリアが増加します．

このとき，ＰＮ接合部に存在するキャリアの電荷量は，フェルミ・ディラック分布（外部バイアスに対する電子濃度の関係）の関係（等）に応じています．フェルミ・ディラック分布は，Exponential 関数です（詳細はこちら）ので，電位差に対するキャリア濃度分布もExponential 関数になります．

一般に物質中の電流は，キャリア濃度およびキャリアの移動速度に比例します．また，キャリアの移動速度は物質中の電界に比例の関係があります（詳細はこちらを参照）．

ダイオードの I-V 理論関数は，この関係（式1-2-7）とフェルミ・ディラック分布関数とから導くことができると思います．筆者は計算してませんが，たぶん．．．

回路設計の現場では，ダイオードの I-V特性の関係式は，単純な指数関数によって近似することが多いので次式3-2-5を紹介しておきます．

I_S（飽和逆方向電流）は，大きな逆バイアスを与えたときに流れる逆方向の電流（スカラー）です．これは，少数キャリア（Ｎ型半導体中のホール，Ｐ型半導体中の電子）により通電可能な電流の大きさを想定しています．

順方向バイアスＰＮ電位差を与えるとフェルミ・ディラック分布に従って接合部の障壁を越えることのできるキャリア濃度が，指数（Exponential）関数的に増加します．このキャリア濃度の割合を，少数キャリアに対するバイアスによるキャリア分布増加分の比としてI_S（飽和逆方向電流）に乗じて I_F を求めています．

そのため，式3-2-5の A は，A=e(2.718281828)を中心としたパラメータと考えていいと思います．bは温度に係わる係数です．図3-2-31は，I_Fの温度特性について負の温度係数をもつダイオードを例に図示しています．しかし，一般に市販されているダイオードは正の温度係数をもつものも多くあります．これらのパラメータは現物に合わせて設定しましょう．

式3-2-5の関係は，V_Fの変動が小さいことを前提として近似しています．実際には，上記にもちょっと触れましたが，電界とキャリアの移動速度のパラメータ（これらは一般に抵抗率に集約できる要素）が考慮されていませんので，VFの変動の大きいシミュレーションの場合には注意が必要です．対応としてはダイオードにシリーズに抵抗を挿入を仮想的にすることによってより現実に近いI-V特性をつくることができますので必要に応じて設定しましょう．

← 戻る  1  2  次へ →