2次系伝達関数の特徴2
伝達関数の一般式(下式2-3-30)のパラメータとシステムの物理的特徴との関係を前回解説しました(こちら参照).特に減衰比ζは伝達システムにおいて振動に関係しているパラメータです.
| |
式2-3-30 |
ここでは,減衰比ζについて具体的に特徴をとらえていきましょう.
図2-3-20は,式2-3-30の伝達システムについて,ζの値別にステップ応答の過渡波形をグラフに示しています.
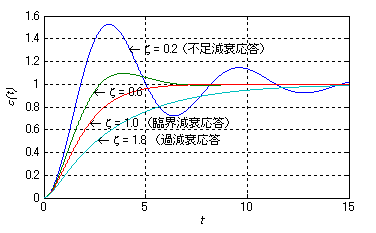
図2-3-20 2次系伝達関数の過渡応答
条件:
ωn=1
ωn=1
先述の通り,減衰比ζに応じて振動減衰が調整された波形が得られます.ここで振動の減衰に関してζの範囲と過渡応答の関係が表のように名前が付けられています.
| 減衰比ζ | 応答 | 過渡式 |
| ζ<1 | 不足減衰応答 | 式2-3-36 |
| ζ=1 | 臨界減衰応答 | 式2-3-37 |
| ζ>1 | 過減衰応答 | 式2-3-38 |
表2-3-2 減衰比ζと応答
つぎに,減衰比ζが振動の大きさを調整しているターゲットとなる振動周波数を考えます.
振動条件であるζ<1における過渡関数は次の式2-3-36でした.
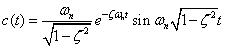 |
式2-3-36 |
この式過渡関数からは振動周波数は,ζ=0でωnとなり,ζ→1で0 に近づくことが分かります.しかし,周波数応答からζによる振動の調整を考えたとき見方が変わってきます.
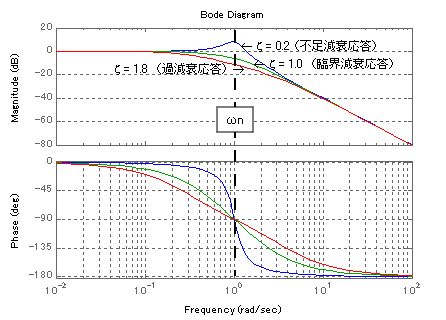
図2-3-21 2次系伝達関数の周波数応答
図2-3-21は,2次系伝達関数(一般式)の周波数応答を示しています.位相(Phase)に着目するとζの値を問わず,固定角周波数ωnがいずれも位相変化点の中心になっています.
振幅利得(Magnitude)をみると,固定角周波数ωnの周波数がζに応じてゲイン調整がされている様子が分かると思います.