極と零点1
図2-3-16に例示する回路について周波数特性を考えてみましょう.
| R(s) → | 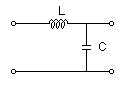 |
→ C(s) |
図2-3-16 回路例1
まず,伝達関数を求めると, (伝達関数の求め方はこちらを参照)
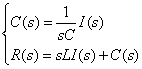 |
式2-3-20 |
より,伝達関数は(途中計算はこちら参照)
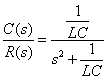 |
式2-3-21 |
式2-3-21の伝達関数をフーリエ変換して周波数関数を求めると(伝達関数のフーリエ変換はこちらを参照)
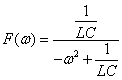 |
式2-3-22 |
これをBode線図に示すと
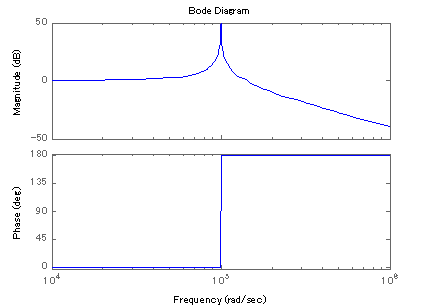
図2-3-17 Bode線図
条件:
L=100[μH]
C=1[μF]
L=100[μH]
C=1[μF]
上図Bode線図は,ω=105[rad/sec]にピークゲインをもつ特徴を示しています.この例示している回路はLC共振回路ですので,共振点をもつことに疑問は無いと思います.
そこでピークゲインは,式2-3-22の分母が0になる点(ゲインは∞[dB])となります.ちなみに,ゲインピークとなる角周波数は
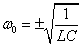 |
式2-3-23 |
この回路例のように,伝達関数が∞のゲインをもつ点を制御工学の分野では極といいます.