フーリエ変換とラプラス変換2
フーリエ変換の電子回路への応用を考えます.一般に過渡現象や制御分野など多くの電子回路計算にラプラス変換が用いられています.ここでは,ラプラス変換とフーリエ変換の共通の特徴に着目して,ラプラス関数(sの関数)から周波数関数を得られる便利な関係について知りましょう.
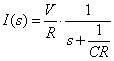 |
式2-2-34 |
これを逆ラプラス変換して時間関数で示すと
![]()
まず,この時間関数(式2-1-22)を通常のフーリエ定義式に従って,フーリエ変換してみましょう.
i は,時間 t が0[s]をスタートとして∞[s]までを対象とする時間関数なのでフーリエ変換する上で次のような定義を必要とします.
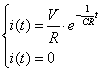 |
|
式2-2-35 |
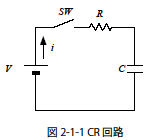
t が0s 以前は,図2-1-1のSWがOFFとすると,回路に電流は流れませんので,(t < 0)においてi(t)=0 となります.フーリエ積分を積分範囲ごとに分解してしめすと
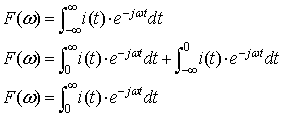 |
式2-2-36 |
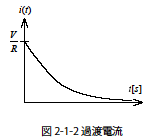
よってこの過渡関数のように(t < 0)の範囲で i(t)=0 となる関数の場合,式2-2-36のようにフーリエ積分の範囲を( 0≦ t ≦∞)としても結果は変わりません.
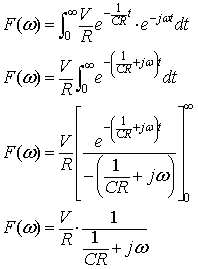 |
式2-2-37 |
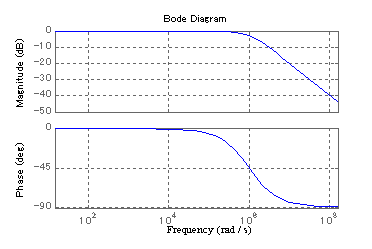
V=1[V]
R=1[Ω]
C=1[μF]
図の詳細は別途解説
つづいてラプラス関数とフーリエ変換の関係について考えます.上記例題の過渡現象のようにフーリエ積分の範囲を[0:∞]にできる場合,ラプラス関数から簡単にフーリエ変換することができます.
ラプラス変換定義は次のように与えられていました.
![]()
複素数s (s = σ + jω)について展開すると次のように示すことができます.
| |
式2-2-33 |
ここでちょっと強引ですが
σ=0 すなわち s=jω とすると
式2-2-33は次のようになります.
| |
式2-2-38 |
ここでフーリエ積分の範囲を[0:∞]にできる場合のフーリエ変換定義式は
| |
式2-2-39 |
ですので 式2-2-38と式2-2-39は,f(t)に対して全く同様の変換を行っていることになります.
そこでフーリエ積分の範囲を[0:∞]にできる場合でかつ,フーリエ積分で収束する条件において,ラプラス関数から
| s = jω | 式2-2-40 |
として単純にs にjωを代入することでフーリエ変換することができてしまいます.たとえば上記例題の場合,式2-2-34のsに式2-2-40を適用すると
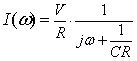 |
式2-2-41 |
フーリエ変換を普通に行った式2-2-37と全く同じ結果が得られることが分かります.
電子回路設計では,制御など多くの分野でラプラス関数を直接扱うケースが多いので,一般に周波数関数を求める場合,フーリエ変換の定義式による正規の方法を使うよりも,上記の方法による(ラプラス変換を介し,ラプラス関数から周波数関数を得る)頻度の方がはるかに高いと思います.
【質問】2009/03/24
図2-2-12の横軸の周波数(Frequency)の意味がわからないです.
図2-1-1の電圧源は直流電圧源(の記号)なので,周波数という概念が回路図を見る限りでは出てこないと思うのですが…….
【回答】2009/03/24
この記事では,図2-1-1中の i 過渡電流に関して解説しています.
回路に与える電圧が直流であれば,流れる電流が直流であるとは言えませんよね.たとえば,L,C直列の系に直流電源をSWを介して接続 した系では,SWオンによって正弦波交流の電流が流れますので.
この記事のように,電流等を時間を引数とする関数で与えられる場合には,フーリエ変換等によってこの電流に含まれる周波数成分を 数学的に解析することができます.