フーリエ変換とラプラス変換
フーリエ変換とラプラス変換の関係を考えます.フーリエ変換とラプラス変換は次式で与えられました.
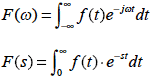 |
式2-2-20 式2-1-8 |
(上式がフーリエ変換,下式がラプラス変換)ここでラプラス変換におけるsは一般的に複素数です.そこで s を実数と虚数に展開すると
s = σ + jω
とすると,式2-1-8 は次のように示せます.
| |
式2-2-33 |
こうして式2-1-8を展開すると,ラプラス積分の中に, e-jωt の要素を含み,積分範囲の違いはあるものの,フーリエ変換の要素も包含しているとイメージ的に捉えることができると思います.
ところでラプラス変換の σ は,
σ > 0
と定義されています.
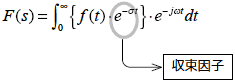 |
式2-2-33 |
ここで, e-σt に着目すると,時間tが大きくなるとともに小さくなり,その結果式2-2-33の積分の収束に起因します.そこでこの e-σt を収束因子と言います.
ここで,式2-2-33(ラプラス変換)は f(t)のフーリエ変換に収束因子を乗じたものと考えることができます.この収束因子を与えることによってより広い範囲の関数を複素領域に変換することができます.
しかし,式2-2-33の時間領域を負の領域にまで拡張すると,収束因子のe-σtは反対に時間t が小さくなるに従って大きくなりラプラス積分は収束できません.よってラプラス変換は収束因子の設置に応じて収束を目的とした積分範囲[0,∞] を設定しています.