ラプラス変換の定義
ラプラス変換は数学的意味を掘り下げると非常に深く，利用される例は多岐に及ぶため，このセクションでは電子回路の過渡現象に関する微分方程式の解法への利用に限定して説明していきます．
ラプラス変換の定義は，時間t の関数をf(t) とすると
のように与えられます．この式は時間t の関数f(t) に
を掛け合わせたものについてt=0 から∞ までを積分することで t の関数を s の関数F(s) に変換するものです．この変換をラプラス変換といいます．式中のs はラプラス演算子といいs>0で複素数も取り得ます．式2-1-8のラプラス変換を数式記号を用いて示す場合は次のように記します．
ラプラス変換された関数 F(s) を時間関数 f(t) に再び変換することをラプラス逆変換といいます．式2-1-9のラプラス逆変換を数式記号を用いて示す場合は次のように記します．
微分方程式を解くためには，上記のラプラス変換とラプラス逆変換を対で使用して解いていきます．一口でいうと，時間t の領域における問題をラプラス変換により実数または複素数 sの領域に変換して，s 領域における問題に置き換えた上で，その問題の解をs領域で代数的に求め，再びs領域の解をラプラス逆変換により時間t の領域に戻す数学的手法です．
ラプラス変換のイメージを絵的に説明すると，ラプラス変換によって得られるF(s)はf(t) と とを掛け合わせたものについてt 軸に挟まれたt=0 から∞までの面積と考えることができます．
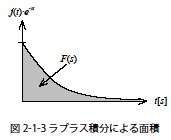
具体的に図を使って説明すると図2-1-3のグラフは時間関数 f(t)と とを掛け合わせたもの（ラプラス積分の中身）について，時間的変化を示したものです．図2-1-3の灰色に塗りつぶしている領域の面積がまさに式2-1-8定義で示しているF(s)と等価のものです．
ただし図2-1-3はf(t)· がt →∞で収束するケースを示しています．このようにラプラス変換するためにはラプラス積分値（F(s)）が収束することが絶対的な条件となります．
というかむしろラプラス変換は を掛けることによって関数f(t)の収束条件を緩和させる働きをしています．このように収束に起因する因子（ラプラス変換における）を収束因子といいます．
ラプラス変換できない例としては，f(t)=exp(t t )の場合，（exp(x)はexと同じ）ラプラス積分が∞に発散してしまうので，ラプラス変換することはできません．