フーリエ変換
これまで,周期のある関数を対象に,その関数に含まれる直流成分と振動成分(sin,cos )への分解についてフーリエ級数展開と,フーリエ係数,スペクトルのセクションで説明してきました.ここでは周期の無い関数を考えてみましょう.
下式は複素表示されたフーリエ級数展開とフーリエ係数です.
| 式2-2-10 |
これまで,基本となる繰り返し周期をT として有限の値としてきましたが,ここでは,周期のある関数式を周期の無い関数も扱うことができるように,繰り返し周期T をT→∞ として考えることにします.
まず,式2-2-10に式2-2-12を代入すると
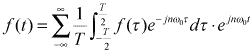 |
式2-2-13 |
T→∞の極限値を求める前に,この式の意味について考えておきましょう.まず,上式の式2-2-12の部分については,f(t)を構成する周波数成分nω0の成分の大きさを抽出したフーリエ係数になります.そして,式2-2-10の部分で先に求めたフーリエ係数を,ふたたび各振動成分ejnωt(ejnωt=cos nωt +j sin nωt)に掛け,すべての振動要素を足しあわせて元々のf(t)を復元しています.
これから式2-2-13についてT→∞の極限値を求めます.
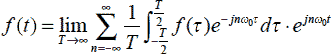 |
式2-2-14 |
ここで周期T と基本波成分の角周波数ω0 の関係は![]() なのでΣ内の(1/T)は
なのでΣ内の(1/T)は
| 式2-2-15 |
とします.
これによって,eの乗数にあるnω0は,nΔω0となります.nω0は,もともと周期関数の繰り返し基本(角)周波数に整数n をかけた離散した周波数です.T→∞の極限によってΔω0→0となり,さらに,n は −∞ 〜 +∞の範囲に無限に分解されるものなので,nΔω0は離散した周波数から連続した周波数として扱うことができます.そこで,nΔω0は
| ω = nΔω0 | 式2-2-16 |
とします.よって式2-2-14は次のようになります.
| 式2-2-17 |
| 式2-2-18 |
ここでこの式の意味を考えましょう.先ほどの式2-2-13で周期f(t)についてフーリエ級数展開してふたたび元々のf(t)に復元していました.式2-2-18も考え方は同様で,二重積分の中にある一般関数f(t) が,
f(t) → 変換 → [変換された関数] → 復元 → f(t)
の2重の変換の手順を経て,元々の関数f(t)を復元していると考えることができます.そこで,
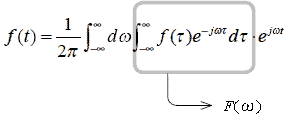
上記の枠線内τによる積分に着目すると,この積分が積分可能で発散しないものとすれば,t[-∞,∞]の積分値はωの関数になることがわかると思います.
そこで上記枠線内をF(ω)とおくと式2-2-18は
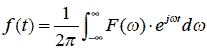 |
式2-2-19 |
この関係式は,(角)周波数領域の関数を時間領域の関数へと変換していることがわかると思います.この式2-2-19 はフーリエ逆変換と定義されています.また式2-2-18 から式2-2-19 への変化で導入した
| 式2-2-20 |
この関係式は,時間領域の一般関数を周波数領域の関数へと変換しています. この式はフーリエ変換と定義されます.
【質問】2008/06/11
式2-2-15のT→∞に向かうときに構成される式が理解できません。もしよろしければもう少し詳しく説明していただけないでしょうか。 また「周波数成分」を英語でいうとなんて言うのでしょうか。 よろしくおねがいします。
【回答】2008/06/12
2つのご質問それぞれについて回答いたします.
- 式2-2-15の解説
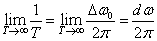 式2-2-15
式2-2-15
まず,この式が導入される目的について触れます
Tは,フーリエ係数(振動成分の大きさに対応する要素)を求めるための時間範囲を設定しています. フーリエ係数を求める対象とする周波数は,このTを周期とする基本波と,その基本波の周波数のn倍(n=1,2,3・・・)の周波数をもつ波となります.
要するに,フーリエ係数の引数であったとびとびの周波数を,連続的なものに変換したいということが目的にあります. そこで,T→∞としてフーリエ係数の引数(周波数)を連続するパラメータに対応させる.というのがこの式の背景です.
それがわかれば,式2-2-15の式自体は難しくないと思います.f=1/T, ω=2πfなので
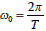
よって
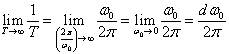
Tをωに置き換えて,さらに極限値をとり微分方程式に変換しています.
-
「周波数成分」の英訳
専門外のことですので,回答しない方針としています.間違ってかえってご迷惑をかける可能性もありますのでご理解いただきたいと思います.