フーリエ係数

周期関数f(t) がフーリエ級数展開可能な場合，上式のようにa₀の直流成分と正弦（sin）波，余弦（cos）波の要素に分解できます．sinおよびcosの大きさ成分（この式におけるa_n，b_n）をフーリエ係数といいます．このページではa₀の抽出，a_nの抽出，b_nの抽出，それぞれの抽出方法について考えます．

(1) a₀の抽出

a₀はf(t)を構成する直流成分で，その他はsin ，cos のプラスマイナスを交番する成分になります．そこでa₀の抽出にはf(t) の繰り返し周期（T とする）の時間範囲で積分することでsin またはcos の成分がプラスとマイナスで相殺され直流成分のみを抽出することができます．それを数式で示すと

　　

式2-2-4

(2)a_nの抽出

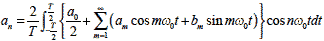a_nはf(t)を構成するcos nω₀tの大きさを示す成分です．このa_nを抽出するためには，f(t)にcos nω₀tをかけたものを基本周期T 間で積分します．

式2-2-5

すると，a_nに掛かるcos² nω₀tの成分は常にプラスとなり基本周期T で積分するとa_nに関わる要素を抽出できます．

一方その他の成分，a₀（直流成分）についてはcos nω₀tを掛けることにより正負を交番し，基本周期Tで積分することによって正負で相殺し0になります．

さらにsinの成分と，cosの成分（cos nω₀t以外）についても，cos nω₀tを掛けても正負を交番する波形となります．これも繰り返し周期T の間で積分することによって正負で相殺し0になります．

以上の内容を数式を使って説明すると，式2-2-5は次式のように展開できます．

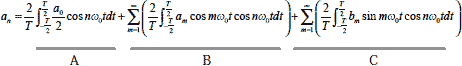
ここで，a₀の直流成分を示す項をＡ，cosの項を B ，sinの項をCと示すと

　・Ａについて

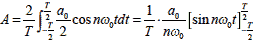
ここで周期T と基本波成分の角周波数ω₀ の関係は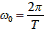なのでＡについては次のようになります．

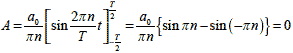	ただし n>0
	ただし n=0

　・Ｂについて

まず最初にcosαcosβ の形を変更します．加法定理より

上式の関係があるので，ＢのΣの中身について変形します．ただしm≠n とします．

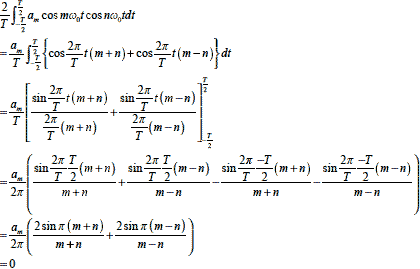
つづいてm＝n の場合

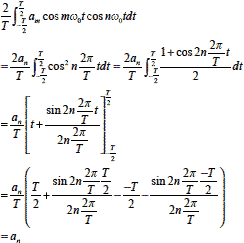
　・Ｃについて

最初にsinαsinβ の形を変更します．加法定理より

上式の関係があるので，ＢのΣの中身について変形します．ただしm≠n とします．

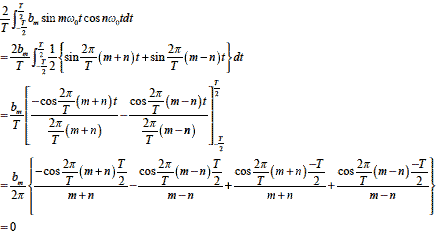
つづいてm＝n の場合

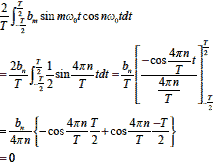
　以上よりa_nの抽出は

	Ａ＝a₀	(n = 0)
	Ａ＝0	(n > 0)
	Ｂ＝0	(n = 0)
	Ｂ＝a_n	(n > 0)
	Ｃ＝0	(n = 0)
	Ｃ＝0	(n > 0)

よって
　　Ａ＋Ｂ＋Ｃ＝a_n
です．ここでanの抽出式（式2-2-5）は，(1)a₀の抽出で導いた関係（式2-2-4）も含む結果となるので統合して

とひとつの式で示すことができ，式2-2-2 のa_nについての関係を説明できます．

(3)b_nの抽出

b_nはf(t)を構成するsin nω₀tの大きさを示す成分です．

式2-2-6

このb_nの抽出はa_nと考え方は同様で，f(t)にsin nω₀tをかけたものを基本周期T 間で積分します．すると，b_nに掛かるsin² nω₀tの成分は常にプラスとなり基本周期T で積分するとb_nに関わる要素を抽出できます．

一方その他の成分である，sinの成分（sin nω₀t以外）と，cosの成分についても，sin nω₀tを掛けても正負を交番する波形となります．これも繰り返し周期T の間で積分することによって正負で相殺し0になります．

数式による説明は，上記と考え方は同様ですので割愛します．b_nは