フーリエ級数
ある一定周期をもつ時間関数f(t) があるとき，その関数が式2-2-1のように三角関数の和に展開することができる場合，その展開をf(t) のフーリエ級数展開といいます．
 |
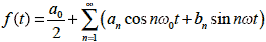式2-2-1 |
上式でn は整数で，n=1,2,3 ･･･∞，t は時間，an，bn はf(t) を構成する正弦波の振幅です．関数f(t) が，電圧や電流などを想定する場合，a0 は直流成分になります．この波の繰り返し周期の成分をもつancosω0t + bnsinω0t を基本波成分といい，ancos nω0t+bnsin nω0t を第n次高調波成分といいます．
フーリエ級数で展開される各高調波成分の三角関数の振幅（式2-2-1 におけるan，bn ），これらをフーリエ係数といいます．フーリエ係数は，波の周期をT としたとき次のように示すことができます．
 |
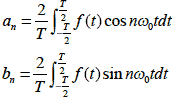式2-2-2 |
式2-2-1フーリエ級数展開について解説
三角関数の和に展開できる波形は矩形波や三角波など単純なものに限定されます．（フーリエ級数展開できないものとしては，繰り返し周期の中でフーリエ係数（an，bn）が時間変化する波形の場合などがあります．たとえば，矩形波，三角波，正弦波など異なる形状の波形が時間的に直列につながれたものが一定周期をもって繰り返す波形などです．）
式2-2-1のa0は，関数f(t)を電圧や電流などに想定した場合，直流成分になります．ancos nω0t+bnsin nω0t は高調波成分の大きさのほか位相成分の情報も含みます．
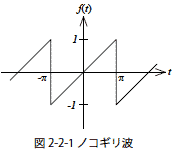
たとえば図2-2-1の波形をフーリエ級数展開すると次式のようになります．
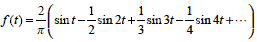式2-2-3
この波形のようにsin の項だけで示すことができる波形もあります．
しかし，位相情報を含めるとsinとcosの両方の項を必要とします．仮に式2-2-1のΣ内をknsin (nω0t＋θ) としてsin の項と位相θ情報におきかえると
knsin ( nω0t＋θ)
加法定理より
＝knsin nω0t cos θ＋kncos nω0t sin θ
ここで
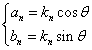
とすると
knsin ( nω0t＋θ)
＝ancos nω0t+bnsin nω0t
ちなみに式2-2-3のようにsinの項のみにフーリエ級数展開できる関数，つまり次式によって示すことができる関数f(t)
を奇関数といいます．つづいて次式によって示すことができる関数f(t)
を偶関数といいます．
【質問】2008/01/09
フーリエ展開の初項がなぜ、2で割ってあるのでしょうか？宜しければ教えてください。お願いします。
【回答】2008/01/09
ご質問の a0/2 は，anを示すフーリエ係数の一般式（次式）からきています．
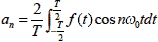式2-2-2この式に直流成分とする，n=0 を代入すると
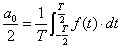
ここで右辺に着目するとちょうど１周期(T[s])間の直流成分を抽出していることがわかると思います． それに対して，式2-2-2の右辺について，n=0としたとき１周期(T[s])間の直流成分の２倍を抽出しています．
そのため式2-2-1において直流成分は a0/2 であるという書き方をして，数学的には式2-2-2と整合しています．