フーリエ変換２

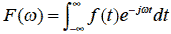式2-2-20

つづいてこのフーリエ変換の定義式（式2-2-20）を使って，次の時間関数を周波数関数に変換してみましょう．

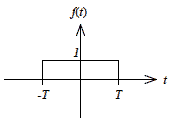
図2-2-2 時間関数

	f(t)=1 (-T≦t≦T)
	f(t)=0 (t<-T,t>T)

式2-2-21

この式2-2-21をグラフに示したものが図2-2-2です．

この関数をフーリエ積分するには，tについて，-∞〜-T，-T〜T， T〜∞ の３つのエリアに分解して考えます．

そこでフーリエ積分を次のように，３つの時間エリアに分解して，シリーズに足していきます．

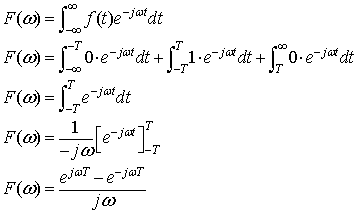
ここでオイラーの関係式より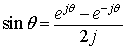なので上式に代入すると

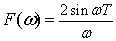式2-2-22

と求めることができます．

下の図2-2-3は式2-2-22をグラフにしたものです．

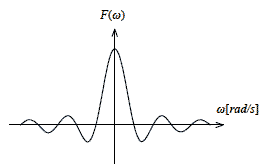
図2-2-3 周波数関数

式2-2-21の時間関数において-T〜Tの範囲が仮に，-∞〜+∞の範囲にまで広げた場合，直流成分のみで交流成分が無いので，周波数特性を考えると，f = 0Hz（ω = 0 rad/s）で F(ω) = ∞の線状のスペクトルをつくることが想像できます．

ところが，その直流成分を図2-2-2のように無限の時間の中から有限の時間を切り取った波形をフーリエ変換すると図2-2-3のような周波数関数が得られ，線状スペクトルにはなりません．

このように無限時間を対象とした場合と，有限時間を対象とした場合とでは，フーリエ変換後に得られる周波数関数に違いが生じるのは，言うまでもなく対象とする時間関数が異なることが起因しています．

実はこうした考え方は，数学だけの話ではなくリアルワールドにおける計測の分野にも関係があります．なぜなら，一般にFFT等で波形をフーリエ変換する場合，無限時間の計測は不可能なので，上記のようにある有限の時間部分をある特定の波形形状で切り取る必要があるためです．

そのため，計測によって得られるスペクトルは，フーリエ変換を対象とする波形が本来の波形とは異なり，本来の姿から切り取られ（加工され）た波形であることが起因し，本来の波形から得られる真のスペクトルとは異なる特性となることを頭に置いておく必要があります．