過渡関数と物理的意味
RLC回路の過渡関数として次の2種類の関数を導出してきました.(式2-1-35についての解説はこちら,式2-1-38についての解説はこちら)
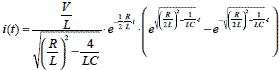 |
式2-1-35 |
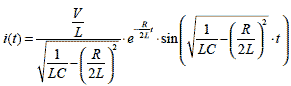 |
式2-1-38 |
これらの過渡関数について次にグラフに示します.
| 式2-1-35 | 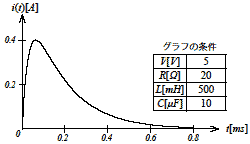 図2-1-7 RLC回路の過渡 |
| 式2-1-38 | 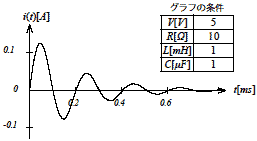 図2-1-8 RLC回路の過渡 |
表2-1-5 RLC回路の過渡
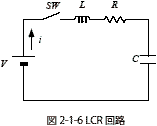
図2-1-7と図2-1-8は同じRLC回路(図2-1-6)について定数が異なる条件での過渡電流波形を示しています.それぞれの過渡グラフは式2-1-35,式2-1-38それぞれから算出していますが,両式は数学的に等価なのでどちらの式を使ってグラフを描いても全く同じ結果にはなります.
図2-1-7と図2-1-8の例は具体的な条件をピンポイントに特定して示していますが,波形を見て読みとれるように振動系と非振動系の条件を代表した条件として示しています.
図2-1-7は
| |
式2-1-40 |
の条件におけるグラフの一例で,図2-1-8は
| |
式2-1-41 |
の条件におけるグラフの一例です.
仮にRLC回路の過渡現象解を式2-1-35,式2-1-38のいずれか一方を解とした場合,上記(式2-1-40,式2-1-41)の条件で虚数(ルート内が負)を含む条件があり物理解としては適当とは言えません,いずれの場合も計算の過程で両式間の展開は必要となります.
ここで着目すべき点は,上記の虚数条件と物理特性の関係かと思います.簡単に言えば式中にsinを「含む」か「含まない」か,式2-1-41の条件では電流は振動し,式2-1-40の条件では非振動(安定)であることが波形を見るまでもなくわかります.このようにRLC回路における振動条件が過渡関数のなかに導き出されていることがわかります.
過渡波形について
t=0s ではコイルの初期電流が0Aなので,回路の接続はコイルを含むすべての部品が直列に接続されているため,i(t) は0A からスタートします.そのときコンデンサC の初期充電電圧は0V なのでコイルL には,電源電圧V がそのまま与えられます.このときのコイルに与えられる電圧は最大となるのでdi/dt(電流の時間に対する傾き)が最大となります.
その後,コイルに電流が流れ始め,このコイル電流がコンデンサC に充電されていき,コンデンサCの充電に共なってコンデンサ電圧が増加して電源電圧V に近づいていきます.
電流の増加にともないコイルにもエネルギー(コイルのエネルギーはこちら(式1-5-57)を参照)が蓄えられます.コイルには,電源VとコンデンサC電圧,抵抗Rの電圧降下との電圧差が与えられるため,コンデンサ電圧が増加するとコイル電圧は徐々に小さくなり,コイルのdi/dt(電流の時間に対する傾き)も減少(コイルの電圧とdi/dtの関係はこちら(式1-5-49)を参照)します.コイル電圧が0Vになる点を境に電流は減少します.
その後,コイルに蓄えられたエネルギーが放出され,di/dt(電流の時間に対する傾き)は負に転じます.図2-1-7の条件では以降,コイルエネルギーは放出され,同時にコンデンサC電圧は電源Vに漸近し回路電流i(t)も0Aに漸近していきます.
図2-1-8の条件では,コイルエネルギーはコンデンサ電圧が電源Vになっても放出しきらずにさらに電圧V以上にコンデンサに充電します.その結果コンデンサ電圧は電圧V以上になりコイルエネルギーが完全に放出された後コンデンサから電源に逆流します.このようにして図2-1-8の条件では振動が見られます.