インダクタンス
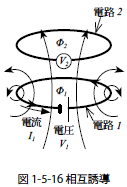
つづいて相互誘導における一次回路に流す電流と二次回路に生じる電圧の関係を求めます.一次回路(電路1)の電流をI1 とすると電路1のつくる磁束に比例関係を持ちます.
![]()
さらにΦ1 とΦ2 には式1-5-40 のように比例関係があるので二次回路への磁束の鎖交数N2Φ2 との関係は

式1-5-44 のようにN2Φ2 とI1 の間にも比例関係が成り立ちます.このときの比例定数をM とすると

となります.このときのM を相互インダクタンスといいます.相互インダクタンスは,一次回路に単位電流を流したとき,二次回路に鎖交する磁束数と定義されています.相互インダクタンスの単位はヘンリー[H] を使います.
相互インダクタンスを使って二次回路電圧V2 を求めると
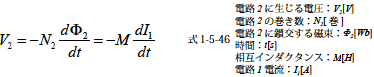
となります.二次回路電圧は相互インダクタンスM に比例し一次回路電流の時間的な変化率に比例します.このようにして2つの導体やコイルの相互の誘導作用をM というパラメータによって単純に一次回路と二次回路の関係を示すことができます.
また,この系を二次回路に電源を接続し一次回路に電圧計を接続したときに誘導される相互インダクタンスは,式1-5-46 に与えられるM と同じ値になります.
先に記した相互誘導の他にも,一次回路がつくる磁束変化が,再び一次回路自身に対しても電圧を誘導します.これを自己誘導といいます.考え方は,先ほどの相互誘導と同じで,ある電路に流す電流I1 によってつくられる磁束がその電路自身に対して鎖交する数をN1Φ1 としたとき

式1-5-47 のような比例関係があります.このときの比例定数をL1 とすると

となります.このときのL1 を自己インダクタンスまたは単にインダクタンスといいます.自己インダクタンスは,ある電路に単位電流を流したとき,その電路に鎖交する磁束数と定義されています.自己インダクタンスの単位は相互インダクタンスと同様ヘンリー[H] を使います.自己インダクタンスを使って誘導される電圧V1 を求めると
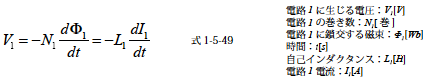
となります.電路の電圧は自己インダクタンスL1 に比例し電路電流の時間的な変化率に比例します.このようにして電路の電流によって生じる電圧の自己誘導作用をL というパラメータによって単純に関係を示すことができます.
つづいて,これまで電磁誘導における各種パラメータの関係を示します.ある相互誘導関係のある一次回路と二次回路があるとき,それぞれの自己インダクタンスをL1,L2 とし,相互インダクタンスをM,結合係数をk としたとき次の関係があります.
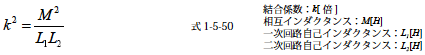
【質問】2008/12/03
自己インダクタンスの説明に関して質問させて頂きます。 「電路の電圧は自己インダクタンスL1 に比例し電路電流の時間的な変化率に比例します」とありますが、時間的な変化率とはどういう 意味でしょうか?これは短時間で変化が行われる程発生電圧が大きくなるという意味でしょうか?また、自己インダクタンスの大きさは 変化する時間の長さに反比例するのでしょうか? ご回答の程宜しくお願い致します。
【回答】2008/12/21
(1) > 時間的な変化率は,短時間で変化が行われる程発生電圧が大きくなるという意味でしょうか?
(2) > 自己インダクタンスの大きさは変化する時間の長さに反比例するのでしょうか?
(1)については,ご質問内で書かれている通りです.
(2)については,自己インダクタンスの大きさは電流の時間的な変化率に反比例する
インダクタンスに関する時間的な電流の変化と電圧の関係は,こちらのコイルの特徴のリンクがわかりやすいと思いますので参照してみてください.