結合係数とインダクタンスの関係

結合係数とインダクタンスの関係についての解説

式1-5-50 について求めます．まず，一次回路に電流変化を与えたときの自己誘導および相互誘導の関係を示します．

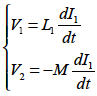
これらの式より

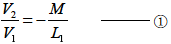
さらに１に式1-5-42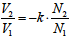，を代入して

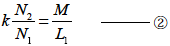
つぎに二次回路に電流変化を与えたときの自己誘導および相互誘導の関係は

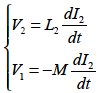
なので，これらの式より?のようになります．

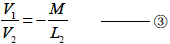
１とは一次，二次が反対の関係になります．さらに結合係数の関係も同様に一次，二次が反対になるので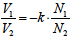，となり，この式より

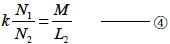
つづいて２式×４式としてお互いの辺を掛け合わせると

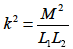
となり式1-5-50 が得られます．