コイルの特徴

コイルに電流または電圧の信号を与えたときに得られる電流，電圧の関係からコイルの特徴について考えてみます．コイルの電圧，電流の関係は次のようにコイル電流の時間的変化が電圧に比例するというものでした．

この式を両辺積分して，積分の形で示すと

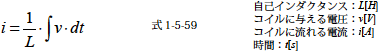
となります．この式はコイルに与える電圧の時間的積分がコイル電流に比例すると解釈できます．ここでV によって積分されるものはコイルの全電路に鎖交する磁束になります．この式はちょうどコンデンサの電流の積分値（電荷量）がコンデンサ電圧の比例関係（式1-4-10参照）と同じ感覚で理解がしやすくなると思います．式1-5-59 は数学的，物理的には式1-5-58 と全く同じ意味をもちますのでどちらを使ってもかまいません．ただ，理解する上では式1-5-59 のように積分型のほうが理解しやすいと筆者は思いましたのであえて示しました．

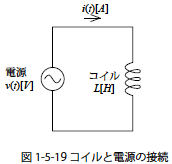
図1-5-19 はコイルと電圧源の接続を示したものです．コイルに与える電圧をv(t)=V として直流電圧を与えたときの電流i(t) は

となります．図1-5-20 はこの式についての電圧，電流の関係をグラフに示したものです．コイル電流i(t) は時間と共に増加する特徴があります．

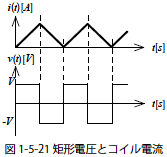
つぎに先ほどの直流電圧を与えたときの電流の関係（式1-5-60）を利用して，矩形波形の電圧を与えたときの波形を図1-5-21 に示します．矩形波形の電圧は一定の電圧値+V，-V を繰り返します．+V を与える時は時間−電流の比例関係によって電流が上昇し，-V を与える時は先ほどの電流と反対の極性になるので負の傾き（時間−電流の比例定数が負）になります．そのため矩形波電圧は三角波電流に変換されます．

つぎにコイルに正弦波交流電圧を与えたときの電流波形を求めます．電圧波形をv(t)=V·cos(ωt)としたとき電流i(t) は

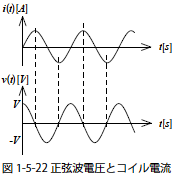
となります．この電圧波形と電流波形をグラフでしめすと図1-5-22 のようになります．正弦波交流電圧をコイルに与えるとコイル電流はやはり正弦波に変換されます．電圧が正である間は電流が上昇し，負になると減少することから，電圧位相に対して電流位相は90[deg] 遅れます．またコイル電流の振幅は式1-5-61 よりであることから，角周波数ω に反比例する特徴があります．これはコイルに蓄えられる磁束が電圧の正弦波周期に応じているためです．

【質問】2009/01/06
図1-5-21において+Vと0(ゼロ）を繰り返し加えたとき、どのような波形になりますか？特に0(ゼロ）にしたとき、どのように計算したら良いのでしょうか？ Ldi/dt=0?

【回答】2009/02/03
コイルの電流とコイル電圧の関係は，式1-5-59の関係に従います．よって直流の電圧がコイルに与えられている間は，図1-5-20のように電圧値に比例してコイル電流が増加します．コイル電圧が0[V]であれば，コイル電流は増加も減少もせずに，電流値が維持されます．

よってご質問のように，コイルに電圧が+Vと0(ゼロ）[V]を繰り返し加えたときには，電圧が与えられているときは電流が増加し， 0[V]が与えられている間は，直前のコイル電流値が維持されます．再び，電圧が与えられているときは電流が増加し， 0[V]が与えられている間は，直前のコイル電流値が維持というサイクルになります．

【質問】2009/02/19
式1−5−58について質問です。
コイルに電流が流れる場合、コイルには誘導起電力が生じるわけであり、式1−5−58の右辺にはマイナス（−）が着くべきだと思っております。なぜマイナスが無いのかが分かりません。幼稚な質問ですが、どうかお教えください。

【回答】2009/02/20

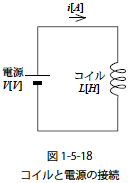
結論から言いますと，式1-5-58にマイナス（−）が着いても着かなくても，式単体だけを論じるのであれば両方問題ありません．電流の流れる向きはどちらかという違いになります．

仮に右図のような，電池とコイルの接続系があったとします．コイルの初期電流が0Aである場合に i に流れる電流の向きを考えた場合，電池の（＋）から（−）の方向（右図に示す矢印の方向）に時間経過とともに増大して流れます．

よって，右図矢印の方向を電流の正として決めれば，式1-5-58のようになります．逆に右図矢印の方向を電流の負として決めれば，式1-5-58にマイナス（−）が着くことになります．

一般に電子回路の分野において，特に条件定義がなければ電源（＋）から電流が流出する方向を正とする場合が，慣習として多く定着しています．たとえば，オームの法則なんかでも，V=Ri としても V=-Ri とはしない方が普通ですね．例外もありますけど．