コンデンサの特徴

コンデンサに電流なり電圧なりの信号を与えたとき，電流，電圧の関係について考えてみます．コンデンサの電荷と電圧の関係は，Q=CV なので電荷量を電流で示すと式1-4-10 のようになります．

　　　

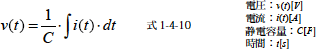
この式からコンデンサの電圧はコンデンサに入力される電流の積分値に比例することがわかります．電子回路を設計においてコンデンサを使用する上で，これは重要で，コンデンサの機能，特徴を示す本質的な関係となります．

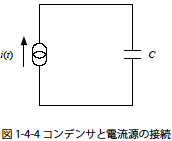
図1-4-4 はコンデンサと電流源の接続を示したものです．図中のはコンデンサの回路図記号です．コンデンサに様々な電流波形を与え，そのときコンデンサに充電される電圧を求めてコンデンサの特徴をとらえましょう．

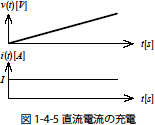
まず，コンデンサに直流電流を与えるときi(t)=I とすると次のようになります．

図1-4-5 は電圧と時間の関係を示すグラフです．コンデンサ電圧は時間に比例して増加することがわかります．

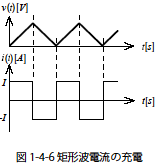
つぎに先ほどの直流電流を与えたときの電圧の関係（式1-4-11）を利用して，矩形波形の電流を与えたときの波形を図1-4-6 に示します．矩形波形の電流は一定の電流値 +I，-I で充放電の繰り返しを想定します．充電時は時間−電圧の比例関係によって電圧上昇し，放電時は充電電流と反対の極性なので負の傾き（時間−電圧の比例定数が負）になります．そのため矩形波電流は三角波電圧に変換されます．

つぎに正弦波交流を与えたときの電圧波形を求めます．電流波形をi(t)=I·cos(ωt)としたとき電圧v(t) は

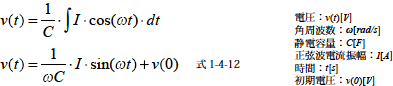
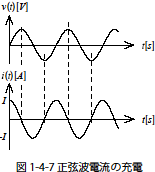
となります．この電圧波形と電流波形をグラフでしめすと図1-4-7 のようになります．正弦波交流電流をコンデンサに与えるとコンデンサ電圧はやはり正弦波に変換されます．

電流が正である間は電圧が上昇し，負になると減少することから，電流位相に対して電圧位相は90[deg] 遅れます．また式1-4-12 から電圧振幅はなので角周波数ω に反比例します．角周波数ω には次のような関係があります．

ω=2πf                      式1-4-13

コンデンサ電圧は充電時間に応じる電荷量に比例するため，充電時間は波形周期に比例関係があるので，周期の逆数である周波数f に反比例します．