コイルのエネルギー
最初に磁界のもつエネルギーについて基本的な概念を知っておきます．ここでの概念はコイルを設計する際，コアの設計において損失計算に必要となる内容です．
先に，電界中の電荷の位置エネルギーについて述べました．それは電界中で電荷を運ぶことに必要な仕事（電位のセクション，およびコンデンサのエネルギー参照）から求めることができました．磁界のエネルギーについては，磁界をつくる際に電路に与えられる電気的な仕事から磁界のエネルギーを求めることができます．そこで図1-5-17 のような無限長の筒状電路によって均一な磁界をつくる際のエネルギーを考えます．そのとき磁界のもつエネルギーを単位体積(1m3) あたりの大きさを考えるため，モデルは，断面積S を1m2 とし，さらに筒の長さを1m として一部分を切り抜いています．
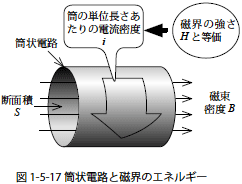
単位体積(1m3)（図の筒状の体積のこと）あたりのエネルギー密度をw[J/m3] としたとき，この磁束をつくる際の電圧を単位面積あたりv[V/m2]，筒の単位長さあたりの電流密度をi[A/m] とすると，仕事は電力（電圧×電流）を時間で積分したものなので次のようになります．
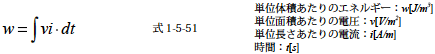
式1-5-51 中の電流密度i[A/m] は磁界の強さを示すH[A/m] と等価（磁界の強さHと磁束密度Bを参照）であるので，i をH に置き換えることができます．さらに電路に与える電圧v は式1-5-39
で与えられます．このときv は単位面積あたりの電圧であるので磁束Φ[Wb] についても，単位面積あたりの磁束である磁束密度B[Wb/m2] を使用します．すると単位面積あたりの電圧v は
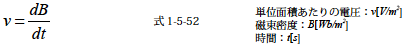
となります．以上を式1-5-51 に導入すると
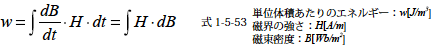
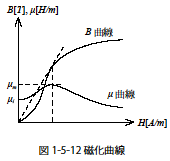
の関係を得ます．この関係は先に述べた磁性材料の磁化（1-5-2 磁性体セクションを参照）において，B軸と磁化曲線に挿まれた面積（図1-5-12参照）を示します．よって，この面積が磁性材料の磁化による単位体積あたりもつエネルギーと等しいことがわかります．
さらにこの式1-5-53 を解くと，B=μH の関係よりつぎのようになります．
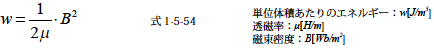
（↑の式1-5-54の関係は真空における条件，μが一定となる場合のみ
△1 訂正(08.3.11)詳細↓）
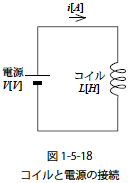
つづいて自己インダクタンスL のコイルに蓄えられるエネルギーを図1-5-18 の系を使って考えます．図中の
はコイルの回路図記号です．コイルに蓄えられるエネルギーも，コイルに対する電気的な仕事から求めることができます．
与える仕事をW[J] とすると次のように示すことができます．
またコイルに与える電圧と電流の関係は
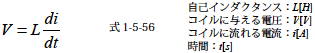
のように与えられるので，式1-5-55 に代入すると
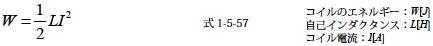
となります．
【質問】2008/03/11
今回の場合は、筒状電路なので、巻数N＝1で、v＝dΦ/dtになると思いますが、単位長当たりの巻数nの場合のコイルだとv=ndΦ/dtで計算するのですか？結果としてw=n(B^2)/2μになりますか？
【回答】2008/03/11> 単位長当たりの巻数nの場合のコイルだとv=ndΦ/dt
> 結果としてw=n(B^2)/2μ
計算上の展開は正しい（△2訂正：詳細↓）のですが，このご質問には，記事の間違いについてのご指摘（あるいは不要な混乱をさせてしまっている）と推測できましたので解説とともに訂正させてください．
まず，記事の間違い部分については，
w=∫HdB 式1-5-53
ここに，B=μHを導入して積分している箇所です．これら両式に間違いはありませんが，μは一般に一定値ではありません．下図参照
唯一真空の条件においては，一定値になりますので式1-5-54が成立します．逆に真空以外の条件では式1-5-54は成立しません．（ここが本記事の訂正個所）
ご質問については，μの扱いに注意が必要です．w=n(B^2)/2μ（△2訂正：詳細↓）ですが，空芯コイルで真空の条件において正しい（△2訂正：詳細↓）ということになります．ご指摘ありがとうございました．
【質問】2008/03/21
2008/3/11の質問をさせて頂いた者です。御回答ありがとうございました。まだ疑問が解けないので、追加で質問させて下さい。
大川電子設計様のように、単位体積当たりの磁場エネルギーを、電圧と電流の時間積分より計算すると、巻数N=nlのコイルの場合、v=NdΦ/dt=nldΦ/dtより、結論としてw=N(B^2)/2μになると思います。ただ、別の導出方法として、コイルのエネルギーU=0.5L(I^2)にL=μ(n^2)Slを代入するとU=(B^2)/2μ×Slとなり、単位体積当たりの磁場エネルギーには(B^2)/2μとなります。これらはどちらが正しいのでしょうか？それともどちらも正しく、現象の捉え方が異なっているだけなのでしょうか？
【回答】2008/04/02
まず，ご質問で想定しているコイルの条件について整理します．
コイルは，空芯無限長ソレノイドとして，その一部分を筒状に切り出して考えるものとして
■コイル条件：
・単位長（1m）あたりの巻き数を n[本/m]
・切り出すコイルの長さを l[m]
・切り出すコイルの巻き数をN[本]
・コイルの断面積 S[m2]
・切り出すコイルの自己インダクタンスを L[H]
・コイル中の磁束を Φ[Wb]
・コイル中の磁束密度を B[Wb/m2]
・コイルに流れる電流を I[A]
ご質問の導出方法は前者と後者２種類ありますが，ここでは前者について説明します．
v=NdΦ/dt
ご質問に記載の通りです．さらにコイルの単位長（1m）あたり，コイルの単位断面積 (S=1m2)あたりのコイル電圧をv1とすると
v1=ndB/dt
よって 断面積 S，コイル長 lのN巻きコイルの vを換算すると
v=nl SdB/dt
つづいて電流について
コイルの単位長（1m）あたりの電流密度をi[A/m]とすると
i=nI
ここで電流密度 i[A/m]は，磁界の強さ H[A/m]と等価ですので次のように置き換えます
H=nI
ここで断面積 S，コイル長 lのN巻きのコイルに外部から与えるエネルギーとして，コイル電圧 vと コイル電流 I の時間積分すると
w=∫vI dt
ここに上記の v，I を代入すると
w=∫nl SdB/dt H/n dt
w=lS ∫H dB
w=lS (B^2)/2μ0
ここで上式を単位体積あたり（l=1m，S=1m2）に換算すれば，
w=(B^2)/2μ0
ご質問のw=n(B^2)/2μは，w=(B^2)/2μ0が正しく電流の換算が不足していたようです．
△2最初の質問に対する私の回答も，w=n(B^2)/2μの計算上正しいと記載の旨間違っていました．w=(B^2)/2μ0が正．併せて訂正します．ごめんなさい
【質問】2008/12/10
コイルに流れている電流を突然切ると、そのコイルに蓄積されたエネルギーは行き場を失ってしまいますよね？ そのエネルギーの行方はどうなるのでしょうか？
【回答】2008/12/13まず，コイルに流れている電流をステップ状に突然切るという動作を現実的に実行できません．電路を遮断するスイッチにもoff時の抵抗値がありますので，その抵抗値とコイル・インダクタンスとの時定数に応じて徐々に電流値が減少していきます．
その時，コイルに蓄積されたエネルギーは，スイッチoff時の抵抗によって消費されることになります．
この現象は，目に見える運動とエネルギーに置き換えてイメージすると，時速60Km/hの自動車が瞬時に0Km/hになったとき，自動車の運動エネルギーは？と問うているのと同様で，自動車が瞬時に0Km/hになることは数学上可能でも現実的には難しいということです．
【質問】2008/12/15
研究で電磁石を作成しようと思ってます。まずは理論値を求めなさいと、指示されました。コイルの磁界の強さを文献で調べると、ほとんどが一重巻きの公式で、H＝niなどと書いてますね。しかし、調べていくとこの公式が使えるのは、一重巻き（単層ソレノイド）の場合だけと、わかりました。多層ソレノイドの場合に使える公式はありますか？
【回答】2008/12/19
電磁石ということなので，有心のコイル（コア有り）ということでよろしいでしょうか．
磁性材料によって磁路を形成すると，一般に，磁束の多くはコアを通ることになります．そのため，簡易的にコアにすべての磁束が流れるものとして近似する場合がよくあります．（磁気回路に関する計算方法を参照してみてください）．
近似が可能になる理由は，一般にコアは比透磁率の大きい物質を使いますので，コアの比透磁率が，μs >> 1 となり，さらにコイル断面におけるコアの比率が大きい場合に，コア外につくられる磁束がコアに通る磁束に対し相対的にとても小さくなり無視できるるためです．このことからご質問にあったように，コイルの巻き方の違いについても（一重巻きか二重かという違いによらず）大きな差は生じにくくなります．
ご質問の公式について，磁気回路が環状であれば磁束密度は概ね下式の通りです．コアの両端の位置が離れている場合には，コア内の磁束分布が一様になりませんので一概に言えませんが，直線状の磁路であればコイル中心付近でのみ，磁束密度が下式で近似できる場合もあります．
B＝μsμ0ni
nはコイルの巻き数
iは電流値