電位

電流は電荷が電気力を受け移動することによって生じます．このような電気力が作用する空間を電界といいます．電界中を移動する電荷は電気的（電界中の力学的）位置エネルギーが高いポジションから低いポジションへ移動したことになります．

このような電界中の位置エネルギーを示す場合，単位電荷(1) あたりの位置エネルギーを使います．単位電荷あたりの位置エネルギーは電位といいます．単位はボルト[V] を使用します．また，ある電位と別の電位の差を電位差または電圧といいます．

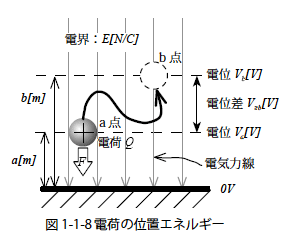
図1-1-8 のような一様な電界Eがあったとき，電荷Q のもつ位置エネルギーを求めます．このとき電荷Q に働く力は一様な電界中いずれの場所でも式1-1-9の関係があります．

F =QE

式1-1-9

電荷の受ける力：F[N] 電荷：Q[C] 電界の強さ：E[N/C]

よってａ点における電荷Q のもつ位置エネルギーは式1-1-10 のようになります．ただし距離0[m] における位置エネルギーは0[J] とします．

式1-1-10

電荷の受ける力：F[N] 電荷：Q[C] 電界の強さ：E[N/C]

a 点における電位（単位電荷あたりの位置エネルギー）Va およびb 点の電位Vbは式1-1-10 より次のように求められます．また，電位差Vba はa 点の電位とb点の電位との差なので式1-1-11 のようになります．

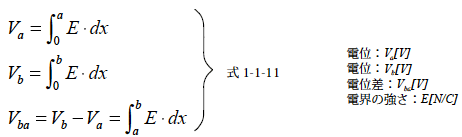
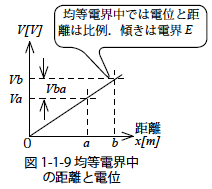
均一電界中では電界E は定数になります．そのため電位と距離の関係は図1-1-8のように比例関係になります．このとき電位Va からVb まで電荷Q を運ぶときの仕事（エネルギー）E_Pb-a は次のようになります．

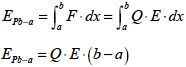式1-1-12

電荷QをVba運ぶ仕事EPb-a[J] 電荷の受ける力：F[N] 電荷：Q[C] 電界の強さ：E[N/C] 距離：a[m] 距離：b[m]

つぎにエネルギーE_Pb-a を電圧，電荷の関係を求めます．式1-1-11 および式1-1-12 より微分方程式を解くと式1-1-13 のようになります．

式1-1-13

電荷QをVba運ぶ仕事EPb-a[J] 電荷：Q[C] 電位：Va[V] 電位：Vb[V]