磁性体

磁界中に物質を置くとその物質が磁化される現象があります.これは物質を構成する原子の構造に要因があります.原子は核と電子で構成され,核の周りを回転する電子による電流や電子の自転(スピン)による電流が磁界をつくります.このようにしてつくられている分子磁石は外部から磁界の影響を受けると方向を変える特徴があります.
この現象を磁化といい,このように磁化される物質を磁性体と呼びます.もともと磁界の影響を受ける前に磁気的に中性であった磁性体は磁化によって,ちょうど磁界中にソレノイドを置きそのソレノイドがつくる磁界が外部の磁界に影響を与えているのと同様な分布をつくります.
そこで磁化された磁性体について磁界と垂直方向に流れる電流ループの成分を抽出したものを想定して,それと等価な電流を流すコイルを考えます.このときこの仮想コイルに流す電流は磁性体の磁化と同等な電流に相当する電流を磁化電流といいます.
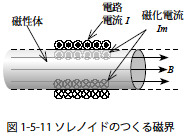
ここで図1-5-11 のように無限長ソレノイドによって均等な磁界を磁性体に与えます.そのとき磁性体の磁化電流をIm として,ソレノイド内部に生じる磁束密度を考えます.ソレノイド内部につくられる磁束密度はソレノイド電路のつくる磁束と磁化電流のつくる磁束の重ね合わせによって求められるので
| B=μ0(NI+NmIm) | 式1-5-32 | 磁束密度:B[T] 真空の透磁率:μ0[H/m] 1m あたりの巻数:N[ 本/m] ソレノイド電流:I[A] 磁化電流の仮想される1m あた りの巻数:Nm[ 本/m] 磁化電流:Im[A] |
となります.ただしN,Nm はソレノイドの単位長さあたりの巻数とします.Nmは図1-5-11 のように仮想して巻かれているものとします.
ここで磁性体の磁化の大きさを式1-5-32 のNmIm に相当するパラメータM の導入をします.同時にこれと同様の物理量で定義され,ソレノイド電流が磁性体に対して与える磁界の強さH というパラメータ(式1-5-32 のNI に相当する)も導入します.すると次のように示せます.
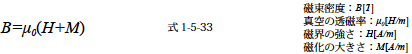
M は外部磁界すなわちH の大きさに応じて変化するのでM はH の関数と考えることができます.よって式1-5-33 を変形すると次のようになります.
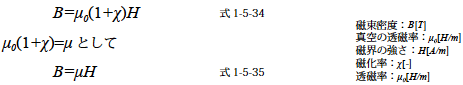
式中のμ を透磁率といい物質の磁気特性によって決まるパラメータです.単位はヘンリー毎メートル[H/m] を使います.ヘンリーという単位は1-5-5 インダクタンスで説明します.また透磁率μ と真空の透磁率μ0 との比を比透磁率といい
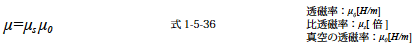
式1-5-36 の関係があります.
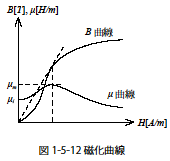
図1-5-12 は磁性体に磁界H を与えたときの磁束密度B および透磁率μ の関係の一例を示しています.図のB 曲線は磁性体の磁束密度を示し磁化曲線といいます.μ 曲線は原点からB 曲線に対して直線を引くときその直線の傾きの大きさを示しています.単純に言うとB=μH のμ を忠実に求めて(微分の傾きではなく切片を含む)グラフ化しています.
H=0 におけるμ の値を初透磁率μi,そしてμ の最大値を最大透磁率μm といいます.このようにコイルやトランスに使用される磁性材料は透磁率が大きく変動します.また温度によっても大きく変動することを知っておきましょう.一方真空中では磁化曲線は直線となり,μ は真空の透磁率μ0=4π×10-7[H/m] となる定数です.