コンデンサのエネルギー
静電容量がC[F] のコンデンサに電圧V[V] の条件で電荷が充電されているとき,そのコンデンサがもつエネルギーを求めます.このコンデンサに蓄えられている電荷をQ[C] とするとこの電荷のもつエネルギーは
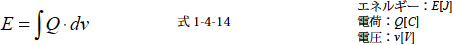
となります(電位セクション式1-1-11 参照).そこで電荷はQ=CV の関係があるので式1-4-14 に代入すると
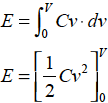
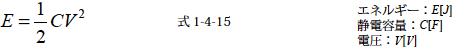
コンデンサのエネルギー(1) は式1-4-15 のようになります.つづいてこの式を電荷量で示すと,Q=CV を式1-4-15 に代入して
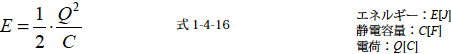
となります.
(1)コンデンサエネルギーの解説
電荷Q が電位V にあるとき,電荷の位置エネルギーはQV です.よって上記コンデンサの場合もE=QV にならえば式1-4-15 にならないような気がするかもしれません.しかし,コンデンサは充電電荷の大きさに応じて電圧が変化するため,電荷の充放電にともないその電荷の位置エネルギーも変化するので単純に電荷量×電圧でエネルギーを求めることはできません.そのためコンデンサのエネルギーは電荷Q を電圧の変化を含む電圧V の関数Q(v) として電圧で積分する必要があるのです.
ここではコンデンサのエネルギーを電圧v(0) から0[V] まで放電する過程でコンデンサのする仕事を考え,式1-4-15 を再度検証します.
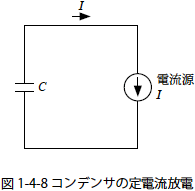
コンデンサの放電は図1-4-8 の系によって行います.放電電流はi(t)=I の一定とします.まず,放電によるコンデンサの電圧と時間の関係を求めます.
より
つづいて電力はp(t)=v(t)·i(t) より
![]()
つぎにコンデンサ電圧がv(0) から0[V] に放電されるまでの時間T[s] を求めます.
![]()
![]()
コンデンサが0[s] からT[s] までの時間に行った仕事を求めます.