過渡関数と物理的意味２
右の図2-1-6のＲＬＣ回路の過渡関数として次の２種類の関数を導出してきました．
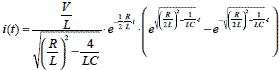
ただし  |
式2-1-35 |
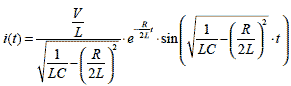
ただし  |
式2-1-38 |
つづいて残る次の条件についての過渡関数を求めます．
 |
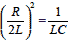式2-1-42 |
上の条件の場合，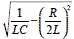
が0 となり，0 による除算の状態になってしまうのでストレートに計算できません．この先は，式2-1-38 から数学的に極限値を求めて解いていく方法と，ラプラス逆変換前に条件（式2-1-42）を代入してからラプラス逆変換をして求める方法があります．ここでは，後者を選択して進めますが，求められる式の妥当性を検証するために前者の方法でも解説(1) をします．
ラプラス変換によって得られた式2-1-37に，条件の式2-1-42 を代入します．
 |
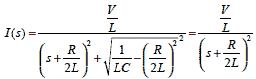式2-1-43 |
この式は，ラプラス変換表（表2-1-3）（下表抜粋）の11に該当するので次式のようにラプラス逆変換できます．
| No | f(t) | F(s) |
| 11 | t eat |  |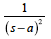
表2-1-3抜粋
 |
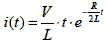ただし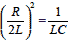 式2-1-44 |
式2-1-44をグラフに示すと図2-1-9の通りです．
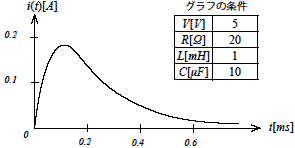
図2-1-9 RLC回路の過渡
(1)式2-1-38から式2-1-44を求める
式2-1-38について極限値をとって式2-1-44を求めます．まずつぎのようにxと置きましょう．
| x = t | |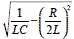
式2-1-45 |
式2-1-38を式2-1-45のxを使って示すと
 |
|
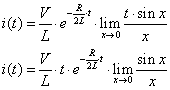となります．ここで極限部は１なので
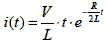
となります．
これでこの回路の過渡電流の関係式をR，L，C のすべての条件において網羅することができました．数学的には解は一つでも可能かもしれませんが，物理現象を扱う場合には，ここで得られた３式のように条件によって使い分ける方が，過渡現象を理解しやすいと思ったので，このように条件別の記述をしています．
このセクションでは，電子回路の過渡現象を数学的にとらえる事によって，おもわぬ回路の特性が導かれていることに気付いたと思います．たとえばR，L，C の非振動条件，振動条件における条件もそのひとつです．
このような特性は，電子回路の設計において，振動または非振動を的確に設計するために必要となる技術です．
ここでは，ラプラス変換を使った応用解析はここで扱った範囲にとどまりません．ここでは，回路の特性を時間関数として求めましたが，ラプラス演算子s を使ったまま，ここで扱ったような過渡や定常における物理的挙動について数学的にさらに深く展開して特性を知ることができます．
その応用（解析）分野は，主に制御工学に学術的に集約されています．特に伝達関数に関する概念はフィードバック技術に欠かすことができません．後々説明したいと思っています．