Twin-Tと2次LPFの組み合わせで減衰特性を改善
| Vin → |
|
→ Vout |
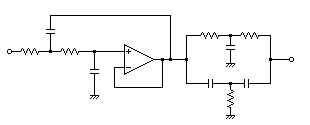
上図の例は正帰還型アクティブ・ローパス・フィルタとTwin-Tノッチ・フィルタの組み合わせですが,ハイパス・フィルタでも可能ですし, 多重帰還型LPF,HPFやその他いろいろな組み合わせが実現可能でその特性も様々につくることができます.
蛇足ですが,上図系のように 0インピーダンスの出力にパッシブ・フィルタ等接続される系では,系全体の伝達関数はそれぞれの伝達関数の積になりますが, 前段にRLCフィルタなど出力のインピーダンスが 0Ωでない系に,Twin-Tフィルタなど,前段の出力インピーダンスの影響を受けます.その影響よってフィルタ特性が変化しますので注意が必要です.
Twin-Tフィルタは,伝達関数に零点を持つノッチ・フィルタで,リジェクト中心周波数においては-∞[dB]を実現できます. そのためリジェクト中心周波数付近では,極めて急峻な減衰特性を得ることができます(Twin-T詳細はこちら). そこで,2次のローパス・フィルタと組み合わせることで,2次の-40dB/decadeの減衰特性に加えて,Twin-Tのリジェクト中心周波数付近の帯域において極めて急峻に減衰特性を得ることになります.
さて図の系で,1kHzをカットオフとするローパス・フィルタの設計例を示します.
| 系 | 設定 | |
| 正帰還型 |
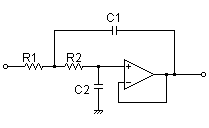 ・カットオフ周波数 fc=1kHz ・クオリティ・ファクタ Q=1.3 |
R1 = 91kΩ R2 = 27kΩ C1 = 0.01uF C2 = 0.001uF |
| Twin-T |
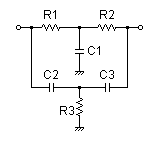 ・リジェクト中心周波数 fc=3kHz |
R1 = 7.5kΩ R2 = 7.5kΩ R3 = 1.8kΩ C1 = 0.01uF C2 = 0.01uF C3 = 0.01uF |
|
− 2次LPF + Twin-T − 2次LPF − Butterworth 4次LPF |
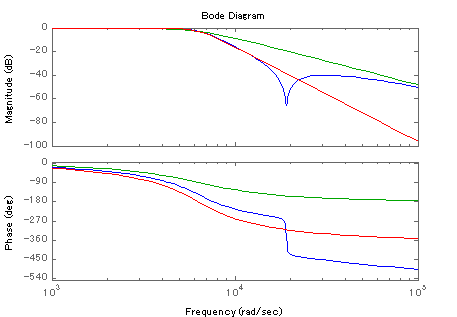
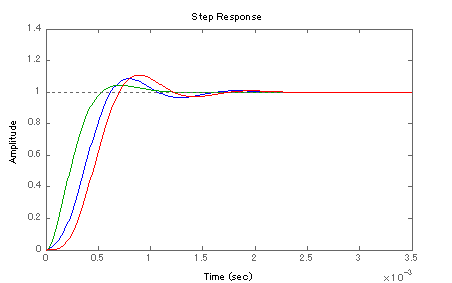
この設定の場合,カットオフ周波数の1kHzから3.6kHz位までButterworth4次と同等程度の減衰特性を示し,3.6kHz以上では,およそ-40dBを維持しています. 実用域では4次と同等程度ですが,位相遅れはButterworth4次よりも小さく(速く)Step応答をみても立ち上がりが速いフィルタであることがわかると思います. ちょっと見た感じでは,楕円フィルタのようなf特ですが,本件は関係ありません.
■本サイトツールによるシミュレーション
この記事に記載の2次フィルタ+Twin-Tフィルタのように,フィルタ系全体の伝達関数をそれぞれのフィルタ伝達関数の積によって 求めることができるフィルタは本サイトのツールの組み合わせによって計算できます.
|
各フィルタ・ツールでカットオフ周波数,Q等の 設計条件をもとに伝達関数を求める |
| ↓ |
フィードバック・ツールで 設定を選択し |
| ↓ |
|
各フィルタの伝達関数をG(s)およびH(s)に入力 伝達関数を合成しBode,Step等の解析ができます. |
現在フィードバック・ツールへの伝達関数の入力は手動ですので,ちょっと手間がかかります. 今後伝達関数のコピーが容易にできるように...ちょっと考えてみます.
カテゴリー:フィルタ(20)
 前の記事
前の記事