20080713
チェビシェフ・フィルタ理論
前の記事
その点がこのフィルタの特徴であり面白さでもあると思っています．チェビシェフとは数学者の名前で，そのチェビシェフさんの考えた チェビシェフ多項式なるものを利用したフィルタが今回のテーマです． まず，はじめにフィルタの考えの基になっているチェビシェフ多項式を知りましょう．
チェビシェフ多項式とは，このようなものです．（チェビシェフ・フィルタにおいて伝達関数の分母に利用されますので頭の片隅に置いてください）
C0(x) = 1
C1(x) = x
C2(x) = 2x2 -1
C3(x) = 4x3 -3x
C4(x) = 8x4 -8x2 +1
C5(x) = 16x5 -20x3 +5x
C6(x) = 32x6 -48x4 +18x2 -1
・
・
C1(x) = x
C2(x) = 2x2 -1
C3(x) = 4x3 -3x
C4(x) = 8x4 -8x2 +1
C5(x) = 16x5 -20x3 +5x
C6(x) = 32x6 -48x4 +18x2 -1
・
・
この多項式は，Cn(x) = cos nθ，x=cos θとしたとき三角関数の加法定理から導き出されたものです． 加法定理について触れておきますと
sin (α+β) = sinα cosβ + cosα sinβ
cos (α+β) = cosα cosβ - sinα sinβ
C0(x)，C1(x)はそのままです．C2(x)は
cos 2θ = cos2θ - sin2θ
cos 2θ = cos2θ - (1 - cos2θ)
cos 2θ = 2cos2θ - 1
cos 2θ = cos2θ - (1 - cos2θ)
cos 2θ = 2cos2θ - 1
C3(x)は
cos 3θ = cos (2θ + θ)
cos 3θ = cos 2θcos θ - sin 2θsin θ
cos 3θ = cos 2θcos θ - (2sin θcos θ)sin θ
cos 3θ = cos 2θcos θ - 2sin2 θcos θ
cos 3θ = cos 2θcos θ - 2(1 - cos2 θ)cos θ
さきほどのcos 2θを代入して
cos 3θ = (2cos2θ - 1)cos θ - 2(1 - cos2 θ)cos θ
cos 3θ = 2cos3θ - cos θ + 2cos3 θ - 2cos θ
cos 3θ = 4cos3θ - 3cos θ
cos 3θ = cos 2θcos θ - sin 2θsin θ
cos 3θ = cos 2θcos θ - (2sin θcos θ)sin θ
cos 3θ = cos 2θcos θ - 2sin2 θcos θ
cos 3θ = cos 2θcos θ - 2(1 - cos2 θ)cos θ
さきほどのcos 2θを代入して
cos 3θ = (2cos2θ - 1)cos θ - 2(1 - cos2 θ)cos θ
cos 3θ = 2cos3θ - cos θ + 2cos3 θ - 2cos θ
cos 3θ = 4cos3θ - 3cos θ
C4(x)はと，．．．
・
・
．．．このままいくと相当なボリュームになってしまうので，cos nθを求めていきます．
Cn(x)すなわちcos nθは
cos nθ = cos {(n-1)θ + θ}
cos nθ = cos (n-1)θ cos θ - sin (n-1)θ sin θ
cos nθ = {cos (n-2)θ cos θ - sin (n-2)θ sin θ} cos θ
- {sin (n-2)θ cos θ + cos (n-2)θ sin θ} sin θ
cos nθ = cos (n-2)θ cos2 θ - sin (n-2)θ sin θ cos θ
- sin (n-2)θ cos θ sin θ - cos (n-2)θ sin2 θ
cos nθ = cos (n-2)θ cos2 θ - 2sin (n-2)θ sin θ cos θ
- cos (n-2)θ (1 - cos2 θ)
cos nθ = 2cos (n-2)θ cos2 θ - 2sin (n-2)θ sin θ cos θ - cos (n-2)θ
- 2{cos (n-2)θ cos θ - cos (n-1)θ} cos θ
- cos (n-2)θ
cos nθ = 2cos (n-2)θ cos2 θ
- 2cos (n-2)θ cos2 θ + 2cos (n-1)θ cos θ
- cos (n-2)θ
cos nθ = 2cos (n - 1)θ cos θ - cos (n - 2)θ
ただし，n≥2
cos nθ = cos (n-1)θ cos θ - sin (n-1)θ sin θ
cos nθ = {cos (n-2)θ cos θ - sin (n-2)θ sin θ} cos θ
- {sin (n-2)θ cos θ + cos (n-2)θ sin θ} sin θ
cos nθ = cos (n-2)θ cos2 θ - sin (n-2)θ sin θ cos θ
- sin (n-2)θ cos θ sin θ - cos (n-2)θ sin2 θ
cos nθ = cos (n-2)θ cos2 θ - 2sin (n-2)θ sin θ cos θ
- cos (n-2)θ (1 - cos2 θ)
cos nθ = 2cos (n-2)θ cos2 θ - 2sin (n-2)θ sin θ cos θ - cos (n-2)θ
sinをcosに変えたいので，sin (n-2)θ sin θを変形します．
cosの加法定理より
cos (n-1)θ = cos (n-2)θ cos θ - sin (n-2)θ sin θ
sin (n-2)θ sin θ = cos (n-2)θ cos θ - cos (n-1)θ
これより
cos nθ = 2cos (n-2)θ cos2 θcosの加法定理より
cos (n-1)θ = cos (n-2)θ cos θ - sin (n-2)θ sin θ
sin (n-2)θ sin θ = cos (n-2)θ cos θ - cos (n-1)θ
これより
- 2{cos (n-2)θ cos θ - cos (n-1)θ} cos θ
- cos (n-2)θ
cos nθ = 2cos (n-2)θ cos2 θ
- 2cos (n-2)θ cos2 θ + 2cos (n-1)θ cos θ
- cos (n-2)θ
cos nθ = 2cos (n - 1)θ cos θ - cos (n - 2)θ
ただし，n≥2
よってCn(x)は，
Cn(x) = 2Cn-1(x) x - Cn-2(x)
から冒頭に記載したチェビシェフの多項式が導き出されるのです．ここまでは高校数学の話．さてこの式がフィルタにどのように利用されるのか？
まず，このチェビシェフの多項式をグラフにしてみると
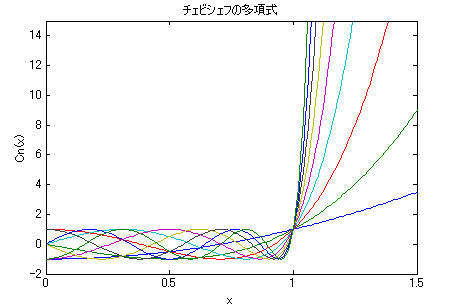
2次から10次までを表示
このグラフ美しいと思えてしまうのは私だけでしょうか？ xが，0〜1の範囲でCn(x)が見事に， -1〜1の範囲に収まっていますね．これは当然，cos nθを求める式ですから， xが0→1は，（x=cos θなので θは，π/4→0に相当する訳なので，）-1〜1になります．xが1より大きい範囲では， 多項式ですから急激に大きくなるという特徴があります．
これはもう，すでにフィルタの片鱗を見せていますよね．このチェビシェフ多項式を伝達関数の分母にしてフィルタをつくっていくのですが， このままでは，対応できません．そこで，このチェビシェフ多項式をフィルタの伝達関数に対応させるために次の施策をします．
- xを周波数ωに対応．伝達関数そのものではなく伝達関数をフーリエ変換した周波数応答にチェビシェフ多項式の特徴をもたせる．
- ωが0〜1における，Cn(ω)の -1から1の間での振動幅（後のリップル：フィルタゲイン振動）を調整する．→εCn(ω)
- εCn(ω)を２乗して使う．目的は， Cn(ω)の負の状態が無いように．
- ε2Cn2(ω)のとりうる最小値を1とする．たとえば， C3(ω)，C5(ω)，C7(ω) のように，ω=0（直流条件）のときCn(ω) が0となってしまう次数では，ローパス・フィルタ（に限りませんが）を形成できないので，次数によらず一律 ε2Cn2(ω)に１をプラスする．
- εCn(ω)を２乗すると，奇数次数のフィルタが実現できないので上記1〜3 を施した全体を0.5乗（ルート）する．
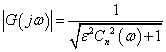---(1)冒頭のチェビシェフの多項式の定義に与えているω = cosθとCn(ω) = cos nθ の形を変えます．cosθおよびcos nθの状態では，1より大きい状態に対応できませんので，cosを含むことのできる等価式に置き換える のです．まず，cos θは，オイラーの関係式から
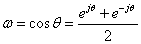
ですが，ここでA=σ+jθとして置き換えます
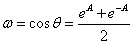σ=0において，この式が成立|σ|>0において，ωが1より大きい状態に対応させます．この発想ちょうど，フーリエ変換からラプラス変換に対応させる術（すべ） に似ていると思った次第（余談）でした．すると上式は
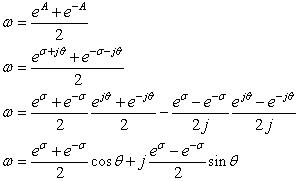---(2)途中cosの加法定理を導入しています
つづいてCn(ω) = cos nθを上記と同様に変形します．
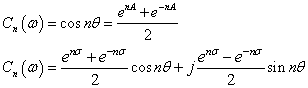---(3)これら(2)(3)式は，実数を示す項と，虚数を示す項に分解されています．さてこれを踏まえて，(1)式から極を求めていきます． これからの筋書きは，(1)を満たす極をすべて求めて（正確には，フィルタ伝達関数が極となるσおよびθの条件）， その極（条件）を直接与えて伝達関数をつくっていきます．フィルタ伝達関数が極となる条件は， [分母]=0なので(1)から．
ε2Cn2(ω) +1 = 0
よって
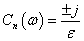
この式に(3)式を導入します．
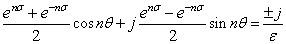---(4)この式より，わかることは左辺の実部が0，左辺の虚部が右辺に等しいことですから．
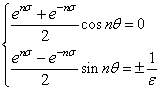
まず，上式ではExponentialの指数関数が0になることはありませんから，cos nθが0ということになります．ので極におけるθの条件が 求められます．
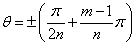---(5)m=1,2,3・・・n
(5)式については，符号の±のうちいずれかを選択する必要があります．θの条件は，1〜nまでのn個存在することになります．
つづいて下式では，(5)式を導入するとsinは -1 か 1 になります．ので
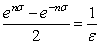
この式をσについて解きます．
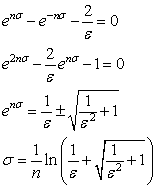---(6)ちょっと戻って，(2)のωの式を伝達関数 sの式に変化させます．一般に 伝達関数からフーリエ変換を行う場合に，s = jωとして簡易的に行う方法があります．ここではその方法を逆に行います．
ω = s / j = - js
これを(2)に代入すると
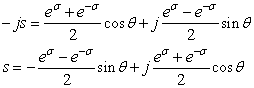---(7)このσとθからsを求める式によって，チェビシェフ・フィルタの伝達関数の極の条件(5)式，(6)式を代入することで極が求められます．
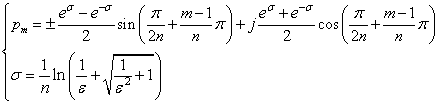--(8)m=1,2,3・・・n
(8)のpm式については，符号の±のうちいずれかを選択する必要があります．極は，1〜nまでのn個存在することになります． （n次のフィルタということですので極の数はn個）
やっとたどり着きました．
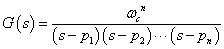---(9)通常，極が求まってしまえば，たとえばローパス・フィルタであれば上式に代入すれば，伝達関数は求められます． もし，実際に(8)を(9)に代入して伝達関数をシミュレーションすれば，(8)式には発振してしまう条件が含まれます．
一般に，極の位置が虚軸より右（実数軸で正の方向）にあれば，系は概ね不安定になります．極の位置が虚軸より左（実数軸で負の方向） にあれば，リアルワールドで負の周波数として信号を与えることはありませんので，系は概ね安定となります．
よって，eσ>e-σであれば， (8)pm式の符号は負，eσ<e-σであれば， pm式の符号は正が選択される必要があります． ちゃんと数式で書けばチェビシェフ・フィルタの伝達関数の極は，次式の通りです．
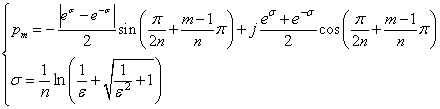--(10)m=1,2,3・・・n
ところで，これまでカットオフ周波数が登場しませんでした．それはこの伝達関数は，正規化（ωc = 1 [rad/s]）された フィルタとして定義していたからです．冒頭でチェビシェフ多項式Cn(ω)の グラフを示して解説したように，ωが1を境に特性が変化する特性をそのまま組み込んでいますのでカットオフ周波数は１[rad/s]となり ます．
では，どのようにカットオフ周波数をスライドするのか？といいますと伝達関数計算ツールにもツールとして組み込んでいますが， 仮に正規化された伝達関数G(s)の周波数特性をωc大きくする方向にスライドするには，G(s/ωc)とします．