20080731
高次ローパスフィルタ伝達関数からハイパスフィルタをつくる
前の記事
これまでチェビシェフ・フィルタの理論とチェビシェフ・フィルタの特徴 について書いてきました．今後，チェビシェフ・ハイパス・フィルタや逆チェビシェフ・フィルタについても書きたいと思っています． 逆チェビシェフ・フィルタを求める際，チェビシェフ・ローパス・フィルタの伝達関数から，ハイパス・フィルタへの変換するような， （利得軸を線対称に伝達関数の変換を行う）過程があります．
ここでは，逆チェビシェフ・フィルタの解説の前に，その方法について紹介しておきます．その方法は，特にチェビシェフに限った 変換方法ではなく，バターワースでも，その他のフィルタでも伝達関数であれば，簡単に実施できる方法です．
ある伝達関数をG(s)としたとき，周波数1[rad/s]を中心に利得軸を線対称に周波数特性を変換するには，（まず，その変換を図で示すと）
|
→ |
|
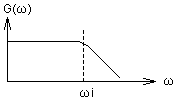
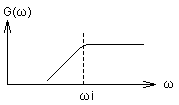
これを式で示すと，もとの伝達関数G(s)は，次のように示します．
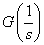
簡単な式で，考え方も単純ですので，解説は必要ないかもしれませんが，さらっと説明しておくと， 1/sを周波数を対数（log）軸で見た場合，
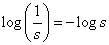
負の成分になり，対数軸ベースで0dBを中心に反転することがわかると思います．反転する中心周波数は，0dBすなわちω=1[rad/s]ですので， 正規化フィルタが対象となります．よって，伝達関数からチェビシェフ・ハイパス・フィルタを設計する場合は， いったん正規化されたローパス・フィルタをつくり，それをハイパス・フィルタに変換するという手続きが効率的です．
その上で，正規化フィルタを任意のカットオフ周波数に変換して伝達関数ベースのフィルタがデザインされる方法が一般的です． 伝達関数計算ツールにこの周波数特性を反転させるツールを追加しました のでご利用ください．
たとえば，チェビシェフ・フィルタの場合，
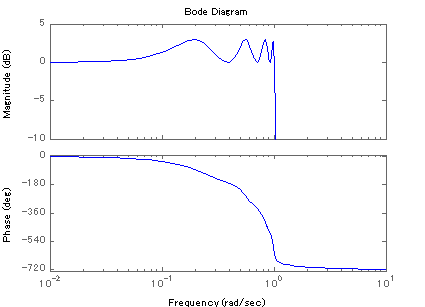
８次チェビシェフ・ローパス・フィルタ
↓
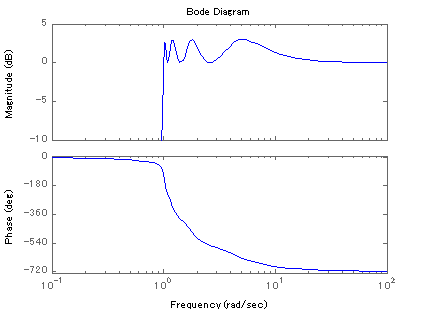
８次チェビシェフ・ハイパス・フィルタ
こんな感じで，周波数軸を高低反転して変換できます．ちなみに，極はこのように変換されています．
|
８次チェビシェフLPF |
→ |
８次チェビシェフHPF |