20080720
チェビシェフ・フィルタの特徴
チェビシェフ・フィルタの極
チェビシェフ・フィルタの理論の解説のなかで,伝達関数の極を求めました. 極は次のツールで計算/グラフにプロットできます.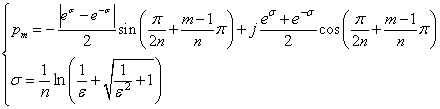 --(10)
--(10)m=1,2,3・・・n
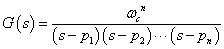 ---(9)
---(9)■n次チェビシェフ・フィルタを構成する一次・二次フィルタのζとωc
※次数とゲイン・リップルを与えて[計算]ボタンをクリックすると,構成する一次,二次フィルタのωcとζ が
計算され列挙され,その条件に応じた極がグラフに表示されます.フィルタ全体としてのカットオフ周波数は,1[rad/s]の
正規化フィルタです.チェビシェフ・フィルタの周波数応答
3,5,7,9次(奇数)チェビシェフ・フィルタの周波数応答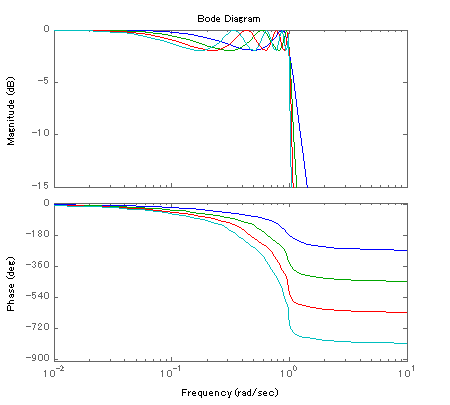
2,4,6,8次(偶数)チェビシェフ・フィルタの周波数応答
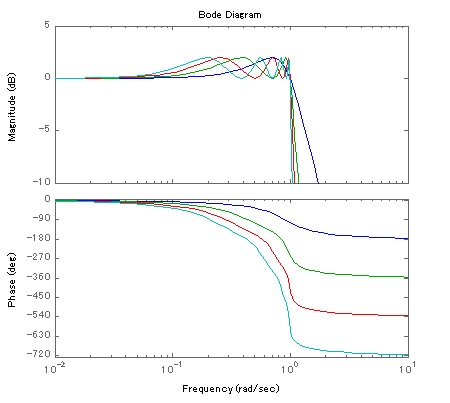
チェビシェフ・フィルタは,カットオフ周波数ωc付近での位相遅れが大きくなることが特徴のひとつです. バターワースの場合は,同じ次数で半分程度ですので...
チェビシェフ・フィルタを構成する各二次フィルタ+一次フィルタは,それぞれのカットオフ周波数ωcmが, フィルタ全体としてのカットオフ周波数ωcより小さく設定されるため,バターワースのように各構成フィルタの カットオフ周波数ωcmがフィルタ全体のカットオフ周波数ωcと同一に設定される場合よりも, 位相遅延が大きくなります.(各カットオフ周波数は上のツールで確認できます).
チェビシェフ・フィルタは,構成する各フィルタのカットオフ周波数ωcmが,全体カットオフ周波数ωcから 離れるほど減衰比が大きく(最大1),近づくほど減衰比が小さく設定されます. 前者の低ωcmによって減衰するゲインを,後者のフィルタの増幅(低減衰比)によって補う構造になります.
チェビシェフ・フィルタのゲイン・リップル
チェビシェフの奇数次数のフィルタと偶数次数のフィルタでは,ゲイン振動のリップルの位置が異なります. 奇数次数では,0dBを境に(対数表現において)マイナス側に,偶数次数では,プラス側に振動するのがグラフから読むことができます.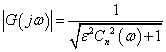 ---(1)
---(1)この特徴は,(1)式のもともとの周波数応答にはありませんでした.(1)式は,次数によらずマイナス側のリップルだけが組み込まれて います.しかし,(9)(10)式の導入によって伝達関数をつくる段階で(1)式の周波数応答が再現されていないのです.それは, 極の情報だけを与えて,伝達関数を設計する場合,フィルタ全体のゲインの情報が織り込まれないためです.(数学的には単に比例ゲイン 1/√(ε2+1)を偶数次数の伝達関数に掛ければ解決しますが...)
| in | → |
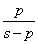
|
→ |
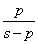
|
→・・・→ |
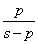
|
→ | out |
上図は,ローパス・フィルタにおける伝達関数の構成で,pは(10)から求められる極です. フィルタを構成するすべての一次フィルタのω=0[rad/s](直流)信号入力時のゲインは,1倍(0dB)になります. よって,フィルタ全体でもω=0[rad/s](直流)におけるゲインは,次数によらず1倍(0dB)になります.
もともと,チェビシェフ多項式(Cn)は-1〜1の振動をもち,チェビシェフ・フィルタでは,同多項式を2乗して使いますので 0〜1の範囲に振動します.ここで,Cn2(ω=0)の値が,nが偶数の場合は 1,nが奇数の場合 0となることから, フィルタ全体の伝達関数の振動としては,ω=0においてゲイン(1倍)を基準にCnの振動が,nが奇数の場合0→1となり, nが偶数の場合は1→0となるため,フィルタのゲイン・リップルが上下に分かれます.
電子回路でチェビシェフ・フィルタを構成する際,偶数次数の場合に,抵抗分圧のような比例ゲインを与えて(1)の理論式に近づけることはできます. しかし,一般に直流(ω=0[rad/s])におけるゲインが1倍にならないため積極的には導入しにくいでしょう.そのため過渡の増幅 (オーバーシュート)を嫌う場合には,奇数次数のフィルタが選択されることが多いと思います.
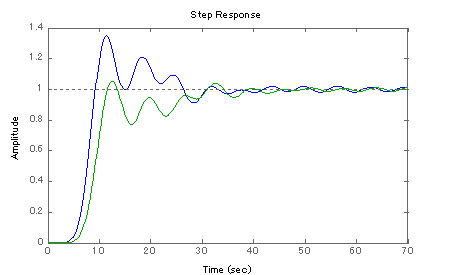
−8次,−9次
8,9次チェビシェフ・フィルタのStep応答
チェビシェフ・フィルタのゲイン・リップルと遮断特性の関係
チェビシェフ・フィルタの周波数応答は,このフィルタのパラメータであるゲイン・リップルによって減衰特性を調整することができます. 下図は5次チェビシェフ・フィルタのゲイン・リップルを振ったときの周波数特性を図示しています.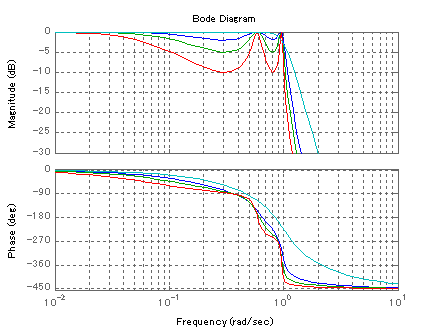
−Butterworth 5次,−リップル2dB ,−リップル5dB,−リップル10dB
ゲイン・リップルが大きく設定されると,フィルタに構成されている一次/二次のフィルタが低いカットオフ周波数に設定されることは
前記の通りで,極プロット(ツール)を見てもわかります.そのため,フィルタ全体として減衰特性が本来,低周波側に設定されている
ことになります.カットオフ周波数ωc付近で減衰比による増幅で持ち上げられていても,その増幅がωc
以上の領域では,急速に減衰してもともとのωcから-20dB/decadeのラインに漸化しますので,フィルタ全体としては,減衰
が低周波化することになります.言いかえれば,より落ちるフィルタに設定できます.
チェビシェフ・フィルタのシミュレーション伝達関数Widgetを使ったチェビシェフ・フィルタの各種応答のシミュレーションです. ■n次チェビシェフ・フィルタのシミュレーション
|
[記事URL] http://okawa-denshi.jp/blog/?th=2008072000
カテゴリー:フィルタ(20)
カテゴリー:フィルタ(20)
 前の記事
前の記事