20080803
逆チェビシェフ・フィルタ理論
逆チェビシェフ・フィルタとは?
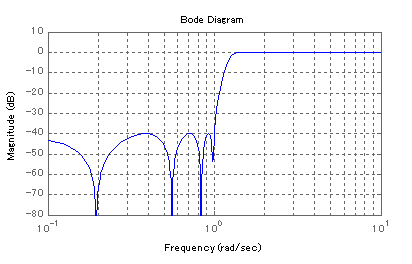
8次 逆チェビシェフ・フィルタ
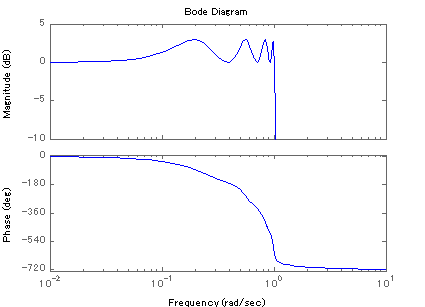
8次 チェビシェフ・フィルタ
いきなりですが,逆チェビシェフ・フィルタと通常のチェビシェフ・フィルタの周波数特性を表示してみました.逆チェビシェフ・フィルタ は上図(上),遮断域に振動があり,透過域がバターワース特性に近いことが特徴です.通常のチェビシェフ・フィルタは,上図(下)のよう にゲイン・リップル振動の位置が透過域に振動があり異なります.また,遮断域では,バターワース特性に近づきます.
逆チェビシェフ・フィルタの理論
以前,記述したチェビシェフ・フィルタは,チェビシェフ多項式を伝達関数に応用したフィルタです. ここでは,このチェビシェフ多項式を応用したもうひとつのフィルタである,逆チェビシェフ・フィルタを解説します.まず,最初にチェビシェフ多項式をおさらいしておきます.チェビシェフ多項式は, Cn(x) = cos nθ, x=cos θとしたとき三角関数の加法定理から導き出されたものです.
C0(x) = 1
C1(x) = x
C2(x) = 2x2 -1
C3(x) = 4x3 -3x
C4(x) = 8x4 -8x2 +1
C5(x) = 16x5 -20x3 +5x
C6(x) = 32x6 -48x4 +18x2 -1
・
・
C1(x) = x
C2(x) = 2x2 -1
C3(x) = 4x3 -3x
C4(x) = 8x4 -8x2 +1
C5(x) = 16x5 -20x3 +5x
C6(x) = 32x6 -48x4 +18x2 -1
・
・
さて,以前解説したチェビシェフ・フィルタは,このチェビシェフ多項式Cn(x)を 次式のように伝達関数の周波数応答に応用しました.
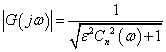 ---(1)
---(1)Cn(x)は,多項式ですので, x>1で急激に大きくなります.よって(1)式は,ω>1で分母が急激に大きくなり 伝達関数としては,ω>1で減衰域になります.
ここでは,このチェビシェフ多項式Cn(x)の特徴を逆に 次のように利用します.
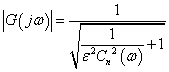 ---(11)
---(11)(1)式に対して(2)式は,チェビシェフ多項式Cn(ω)を逆数にしています ので,ω≤1で 0 ≤ Cn(ω) ≤ 1 ですので, Cn(ω)=0の場合には,伝達関数としては零点となります.また, ω>1でCn(ω)は急激に大きくなり,伝達関数|G(jω)|としては, 1に収束します.
(2)式の設定根拠は,(1)式の設定根拠と共通する部分が多いので,ここでは割愛します.(1)式の設定根拠の解説は,
こちらを参照してください.
よって,(2)式に示す逆チェビシェフ・フィルタ伝達関数は,ハイパス・フィルタとなります.(逆チェビシェフ・フィルタのローパス・フィルタは後述します.) まず,この(2)式の逆チェビシェフ・ハイパス・フィルタの極と零点を求めていきます.
(11)式は,次のように変形できます.
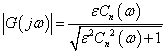 ---(11)
---(11)ここで,分母に着目すると,(1)式と同じであることがわかりますので,極は以前求めたチェビシェフ・フィルタの極がそのまま使えます. よって
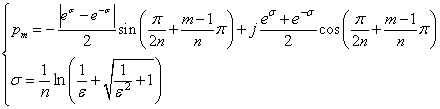 --(10)
--(10)m=1,2,3・・・n
ωとCn(ω)を求めます.両者は, 以前のチェビシェフ・フィルタ理論で求めていますので,引用します. 既読の方は,飛ばしてください.
冒頭のチェビシェフの多項式の定義に与えているω = cosθとCn(ω) = cos nθ
の形を変えます.cosθおよびcos nθの状態では,1より大きい状態に対応できませんので,cosを含むことのできる等価式に置き換える
のです.まず,cos θは,オイラーの関係式から
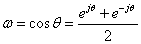
ですが,ここでA=σ+jθとして置き換えます
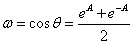 σ=0において,この式が成立
σ=0において,この式が成立
|σ|>0において,ωが1より大きい状態に対応させます.この発想ちょうど,フーリエ変換からラプラス変換に対応させる術(すべ) に似ていると思った次第(余談)でした.すると上式は
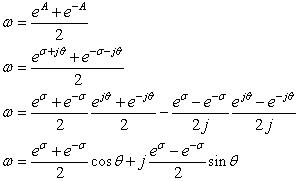 ---(2)
---(2)
途中cosの加法定理を導入しています
つづいてCn(ω) = cos nθを上記と同様に変形します.
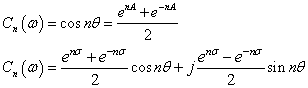 ---(3)
---(3)
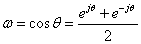
ですが,ここでA=σ+jθとして置き換えます
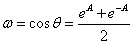 σ=0において,この式が成立
σ=0において,この式が成立|σ|>0において,ωが1より大きい状態に対応させます.この発想ちょうど,フーリエ変換からラプラス変換に対応させる術(すべ) に似ていると思った次第(余談)でした.すると上式は
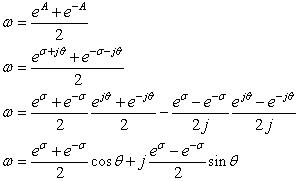 ---(2)
---(2)途中cosの加法定理を導入しています
つづいてCn(ω) = cos nθを上記と同様に変形します.
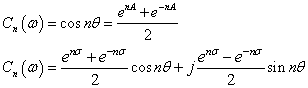 ---(3)
---(3)これら(2)(3)式は,実数を示す項と,虚数を示す項に分解されています.さてこれを踏まえて,(12)式から零点を求めていきます. 零点の条件は,[分子]=0ですから,
εCn(ω)=0 ---(12)
この式に(3)式を導入します.
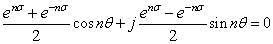 ---(13)
---(13)この式から,左辺の実部および虚部が0であることから.
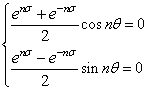
まず,上式ではExponentialの指数関数が0になることはありませんから,cos nθが0ということになります.ので極におけるθの条件が 求められます.
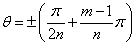 ---(14)
---(14)m=1,2,3・・・n
つづいて下式では,(14)式を導入するとsinは -1 か 1 になります.ので
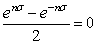
この式をσについて解くと,
σ=0 ---(15)
チェビシェフ・フィルタ極の導出にずいぶん似た展開でしたね.つづいてsとωの関係についても,前記事より引用. 既読の方は,飛ばしてください.
ωの式を伝達関数 sの式に変化させます.一般に
伝達関数からフーリエ変換を行う場合に,s = jωとして簡易的に行う方法があります.ここではその方法を逆に行います.
ω = s / j = - js
これを(2)に代入すると
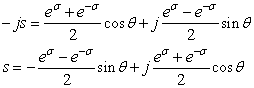 ---(7)
---(7)
ω = s / j = - js
これを(2)に代入すると
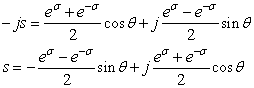 ---(7)
---(7)(7)より,(15)(14)式を導入して零点を求めます.
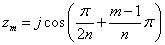 ---(16)
---(16)m=1,2,3・・・n
(10)(16)式から,逆チェビシェフ・ハイパス・フィルタの伝達関数を求めることができます.

上図は,8次逆チェビシェフ・ハイパス・フィルタの周波数応答です.このフィルタは,チェビシェフ多項式をチェビシェフ・フィルタに 対して逆数で利用していますのでフィルタの特性は,ハイパス・フィルタになります.では,ローパス・フィルタは,といますと, 伝達関数に代数的手法を用いて,ハイパス・フィルタをローパス・フィルタに変換する方法があります. こちらを参照ください.
■n次 逆チェビシェフ・フィルタを構成する一次・二次フィルタのζとωc
※次数とゲイン・リップルを与えて[計算]ボタンをクリックすると,構成する一次,二次フィルタのωcとζ が
計算され列挙され,その条件に応じた極がグラフに表示されます.フィルタ全体としてのカットオフ周波数は,1[rad/s]の
正規化フィルタです.|
|
|
逆チェビシェフ・フィルタの伝達関数を求める |
[記事URL] http://okawa-denshi.jp/blog/?th=2008080300
カテゴリー:フィルタ(20)
カテゴリー:フィルタ(20)
 前の記事
前の記事